Generative Model Part 1:Intuition on Latent Variable Generative Model

Generative Model Part 1:Intuition on Latent Variable Generative Model

为了以一种在直觉上更合理的形式去定义生成模型，在 Generative Model Part 0：Theoretical Basis of Generative Model 外再补充一篇 Generative Model Part 1:Intuition on Generative Model 使得生成模型的定义更加的复合直觉上的结果，而不是直接的扔出一堆结果

因为上述的原因，这一篇的叙事语言可能会有一些怪，就像辩论式的语言，这样的叙事方法是符合真理是越辩越明的想法，或者说，这一篇的叙事拟合了笔者在写这一篇时，头脑中两个小人在辩论 X)

Intuition：Every ML problem can be reduced to a fitting problem

在常规的机器模型问题中，我们常努力把问题归结到一种拟合问题上，这种拟合有很多种形式，比如判别模型可以理解成，用一个多层神经网络去学习一个拟合模型，在特征提取器（feature extractor）形成的像空间中，追求对于分离超平面的拟合，而生成模型 \(p_{\theta}\) 在最大似然函数下的定义：

\[\theta^* = \arg\max \sum_i^n p_{\theta}(x_i)\]

看吧，那么这个模型是在拟合什么呢？直觉上很难回答，那么这样定义下的生成模型在直觉上和一般的机器学习模型是产生了分歧的，那么下面尝试用 “拟合XX” 这样的想法来叙事生成模型，同时证明 “拟合XX” 的想法其实和最大似然原则下的模型是等价的

那么借鉴一些判别模型的构造，一个特征提取器 \(f_{\theta}\) ，一个分类器 \(h_{\phi}\) ，\(f_{\theta}\) 执行一个降维的过程，把高维数据流形降维到低维特征空间 \(\Im(f_{\theta})\) 中，进一步的，分类器 \(h_{\phi}\) 在特征空间 \(\Im(f_{\theta})\) 中寻找一个分离超平面，通过超平面判别输入的类别

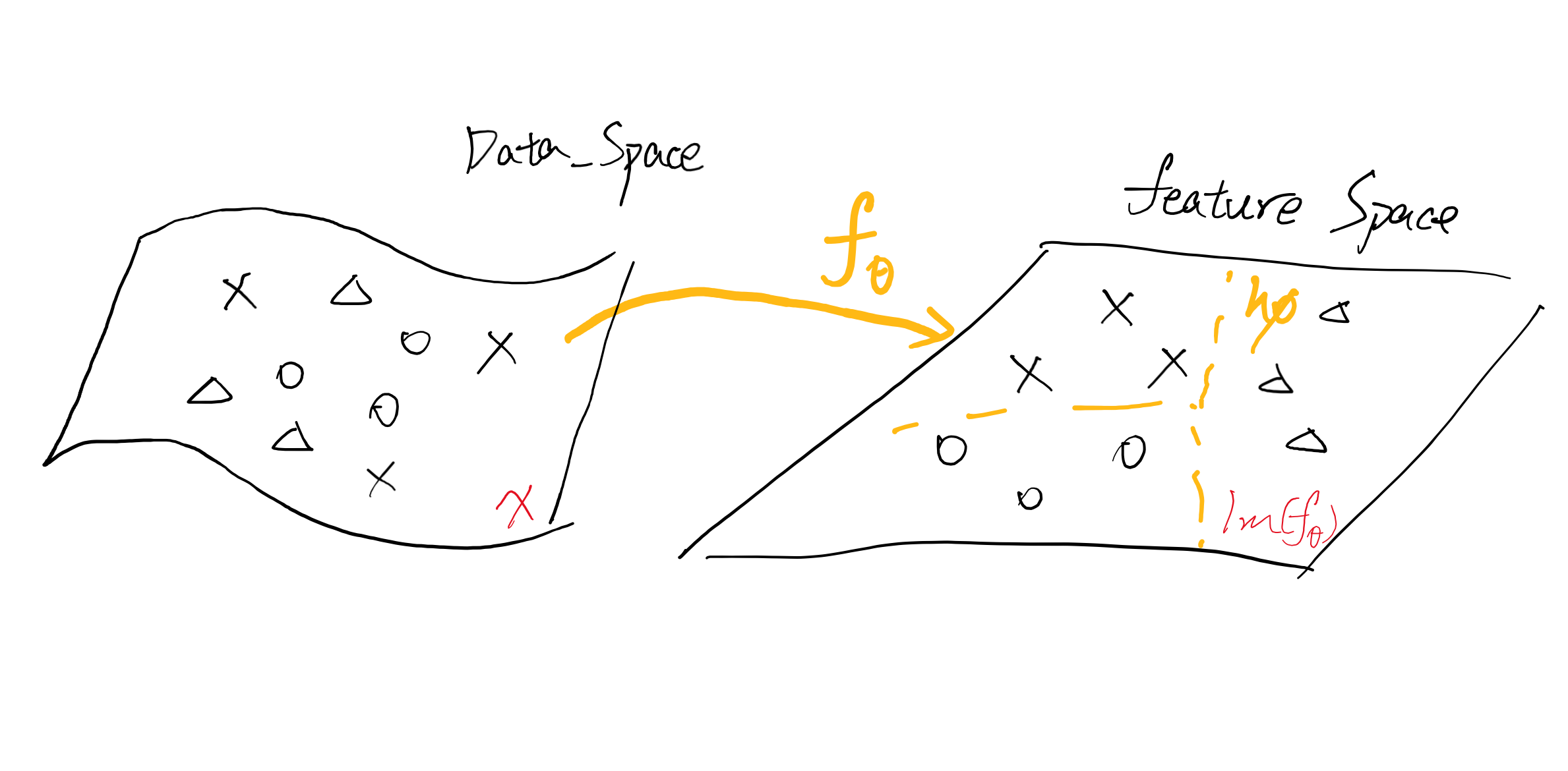
illustration_of_discriminative_model

那么生成模型，或者说基于隐空间的生成模型，其想法是相反的，把低位隐空间中的无意义噪声映射到高维数据流形上，好像是只要一个生成映射 \(g_{\theta}\) 把从隐空间中采样的 \(z\) 映射到 \(g(\theta) \in X\) 中就好了（只要一个参数，事情少了一半），但是并不是，这是训练完的生成模型，但是为了训练生成模型，还需要另外一个参数 \(\phi\) ，“There‘s no silver bullet”

Why latent variable model?

那么按照 “拟合XX” 的思路去构建模型，这件事情是分成两步的，拟合的目标以及拟合程度的度量

但是首先，再往前退一步，要确定是指导建立模型的思想，就是为什么可以通过隐空间构造生成模型这件事情，这是不显然的，有些困惑的，比如拿一个 \(28 \times 28\) 的 \(\textit{minst}\) 字体来说，一种自然的想法当然是：

\[p(x)=\prod_{i=1}^{D} p\left(x_{i} \mid x_{<i}\right)\]

而不是通过隐空间构造的：

\[p(x)=\int p_{\theta}(x \mid z) p_{z}(z) d z = \sum_1^n p_{\theta}(x \mid z_i) p_{z}(z_i)\]

下面那个隐空间的想法甚至都无法顺利的计算（隐空间采样到底多少是合适的呢？）

上面那个分解也是能做的，但是看这个分解就知道，它严重的违反了设计深度学习算法所需要的并行计算的过程，这会导致其计算缓慢

更重要的是，根据隐空间建模这件事情符合一些实验中观察到的事实同时又降低了模型的复杂度：

比如 \(28 \times 28\) 的 \(\textit{minst}\) 字体来说，由于实验上可知，通过判别模型可以对数据进行很好的分类，以tensorflow core提供的网络为例，从特征提取器输出的维度是128维，比起原来的784维小了很多，更不遑论更深的网络，提取器输出的维度比128维还要小很多，这种现象被总结成流形分布律：比起弥散在整个空间中，同源同类的数据更倾向于分布在一个高维流形附近，这支持我们去训练一个复杂度更低的网络，更少的训练量，达到的拟合效果是差不多的
```
class MyModel(Model):
  def __init__(self):
    super(MyModel, self).__init__()
    self.conv1 = Conv2D(32, 3, activation='relu')
    self.flatten = Flatten()
       
    ### just one layer convolution, the complexity of model ###  <- Here!!
       
    self.d1 = Dense(128, activation='relu')
    self.d2 = Dense(10)
   
  def call(self, x):
    x = self.conv1(x)
    x = self.flatten(x)
    x = self.d1(x)
    return self.d2(x)
   
# Create an instance of the model
model = MyModel()
```
那么换一种思路，从仿生的角度来说，我们平时写一个数字，脑子里真的想了784件独立的事情嘛？相反，我们可能考虑笔顺如何？弯折如何？这样的更抽象的事情，而不是思考784个pixel是不是要涂黑。进一步的，若是放大这个数字 \(2\times2\) 倍，难道我们想的事情会多4倍嘛？

因此，通过隐空间来建模生成模型，既有硬件计算上的好处，同时又符合观察到的实验现象，那么好话说完了，该说不好的了，正如之前所说的：

\[p(x)=\int p_{\theta}(x \mid z) p_{z}(z) d z\]

这个式子在计算上是intractability，那么就需要通过绕路的办法来建模遵循隐空间想法的生成模型

What to fit?

根据 “要学习一个好的生成映射” 这件事情来建立一个拟合的目标，仿照之前的判别模型的建立，分成两步来做：

那么如何确定这两步呢？GAN（Generative Adversarial Network）和 VAE （Varaitional Autoencoder）分别提供了两种思路：

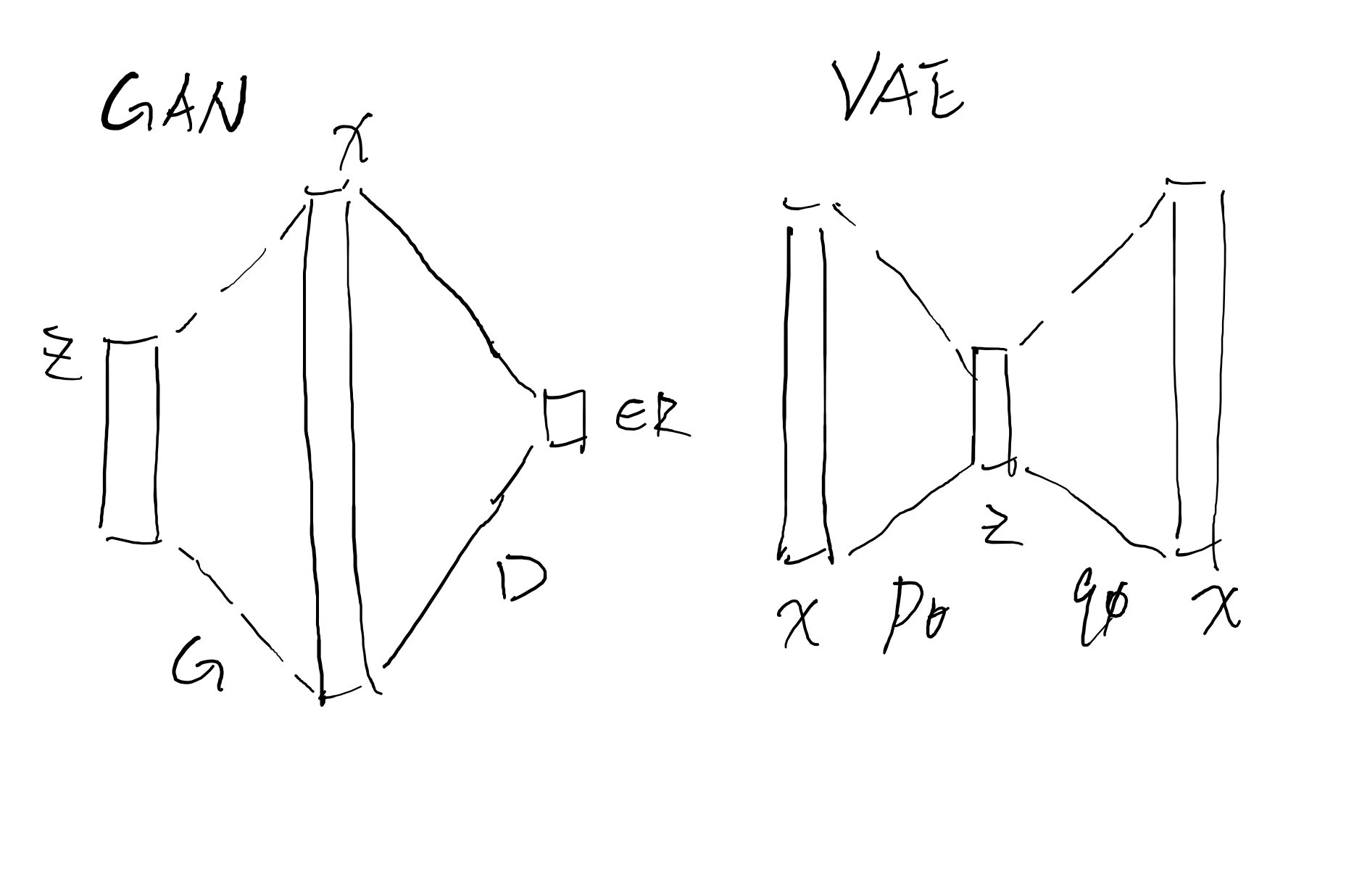
GAN：最后要的是一个好的生成映射，而不是一个真实的数据分布，那么直接追求好的生成映射。第一步通过生成映射 \(G\) 把隐空间采样映射到高维空间中，第二步通过真实数据训练一个度量 \(D\) ，来度量”有多像从数据集中采样的数据”，这样的两步来设计算法
VAE：那么既然有隐空间的想法支持，不妨仿照autoencoder的想法，建立隐空间概率分布和数据空间概率分布的关系，比起GAN放弃了对分布的把握，VAE保留了这一点，在训练过程中，通过编码器 \(p_{\theta}\) 和解码器 \(q_{\phi}\) 来模仿复建的过程，最后从训练好的生成分布中采样，这样的两步来设计算法

画图来说的话就是如下所示：

two_step_GAN_VAE

但是这样看的话，两者在结构上就似乎毫无关系，为了更好的统一起来，需要更高一些的观点，在数据流形拟合这个共同目标下，就能被统一起来：

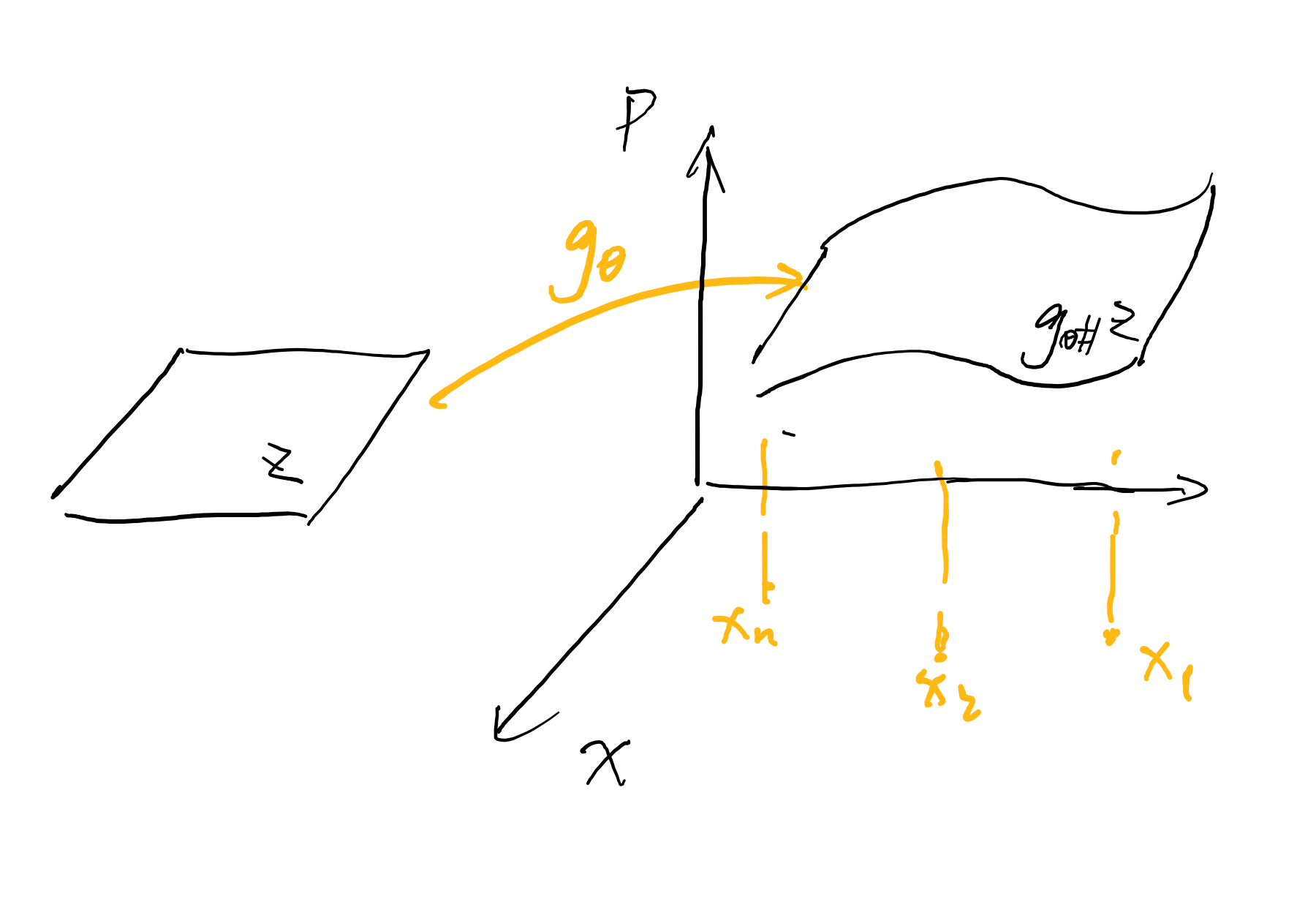
data_manifold_fit

两者都是从隐空间出发，解码器 \(p_{\theta}\) 和生成映射 \(G\) 的作用是类似的，但是区别在于为了度量生成映射 \(G\)，GAN的第二部分需要一个判别器，而相对应的，VAE直接使用原来数据空间中的测度把解码器分布 \(p_{\theta}\) 经验分布比较即可，但是建立隐空间的分布和数据空间的分布之间的双向关系，需要相应的训练一个编码器分布 \(q_{\phi}\)

How good is the fit ?

有了拟合的目标（把数据分布和生成分布进行拟合），就需要去建立衡量拟合程度的指标，接下来把两类模型分开来讲：

Generative Adversarial Network

由于GAN自带一个判别器充当度量，那么现在要做的就是通过判别器 \(D\) 来衡量数据分布 \(p_{data}\) 和生成分布 \(p_{G}\) 之间的距离

Vanilla-GAN

在vanilla-GAN中，goodfellow是利用一种“计数”的思想，构造了一个损失函数，同时证明了构造的损失函数在优化过程中是对于 Jenson-Shannon divergence 的一个逼近：

那么首先从直觉上构造损失函数，我希望判别器提升的话，那么就是分辨的出生成器中出来数据，同时不误判真实的数据，同时生成器要能够尽可能的使生成数据被误认为真实数据，那么减少误分类的数据和增加分类好的数据是判别器的工作，同时生成器就要尽可能骗过判别器

\[\min _{G} \max _{D} V(D, G)=\min _{G} \max _{D} \mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{data}}(\boldsymbol{x})}[D(\boldsymbol{x})]+\mathbb{E}_{\mathbf{z} \sim p_{\boldsymbol{z}}(\mathbf{z})}[1-D(G(\mathbf{z}))]\]

那么这样的损失函数是可以做到要求的，为了不失模型的泛化性，改写成：

\[\min _{G} \max _{D} V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{data}}(\boldsymbol{x})}[f(D(\boldsymbol{x}))]+\mathbb{E}_{\mathbf{z} \sim p_{\boldsymbol{z}}(\mathbf{z})}[f(1-D(G(\mathbf{z}))]\]

这样的判别函数当然是符合直觉的，但是在符合直觉的同时，我们希望在理论给予支撑，换言之，如果这个模型是某种分布的距离的逼近，这样是才是符合理论的方法，而 Vanilla-GAN 中也证明了这一点：

首先固定生成器 \(G\)，去求出最优的判别器 \(D\)：
\[\begin{aligned} V(G, D) &=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x})) d x+\int_{\boldsymbol{z}} p_{\boldsymbol{z}}(\boldsymbol{z}) \log (1-D(g(\boldsymbol{z}))) d z \\ &=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x}))+p_{g}(\boldsymbol{x}) \log (1-D(\boldsymbol{x})) d x \end{aligned}\]
由于 \(y \rightarrow a \log (y)+b \log (1-y)\) 在 \([0,1]\) 上在 \(\frac{a}{a+b}\) 取到最优，因此最优的判别器是 \(\frac{p_{\text {data }}(x)}{P_{\text {data }}(x)+p_{g}(x)}\)
在此之上固定判别器 \(D\)，这其实能够充当一个距离 \(D(p_{g},p_{data})\)：
\[\begin{aligned} D(p_{g},p_{data})&=\max _{D} V(G, D) \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}\left[\log \left(1-D_{G}^{*}(G(\boldsymbol{z}))\right)\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log D_{G}^{*}(\boldsymbol{x})\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \left(1-D_{G}^{*}(\boldsymbol{x})\right)\right] \\ &=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}}\left[\log \frac{p_{\text {data }}(\boldsymbol{x})}{P_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right]+\mathbb{E}_{\boldsymbol{x} \sim p_{g}}\left[\log \frac{p_{g}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_{g}(\boldsymbol{x})}\right] \\ & = -\log (4)+K L\left(p_{\text {data }} \| \frac{p_{\text {data }}+p_{g}}{2}\right)+K L\left(p_{g} \| \frac{p_{\text {data }}+p_{g}}{2}\right) \\ & = -\log (4)+2 \cdot J S D\left(p_{\text {data }} \| p_{g}\right) \end{aligned}\]

那么说明vanilla-GAN在训练过程中本身就是在拟合一个 \(JS\) 散度

Wasserstein-GAN

那么现在回到散度本身，无论是 \(KL\) 散度抑或是 \(JS\) 散度，都可以统一在 \(f-divergence\) 下， \(f-divergence\) 可以充当一个分布之间的距离：

\[D_{f}(P \| Q) \equiv \int_{\Omega} f\left(\frac{d P}{d Q}\right) d Q\]

并且有以下约束：

\(f\) 是凸函数且 \(f(1)=0\)
\(P\) 在 \(Q\) 的意义下，在 \(\Omega\) 上连续

那么先回到之前vanilla-GAN中定义的 \(p_{data}\) ，这个是真实数据分布，这只能说明 \(p_{data}\) 是存在的，而没有提供给我们一个如何 \(p_{data}\) 的办法，那么如何对于 \(p_{data}\) 做一个合理的逼近呢？

经验分布函数可能是一个合理的选择，有数据集 \(X=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}\)，通过 \(\delta\) 函数定义经验分布函数：

\[\mu_{X}(x)=\frac{1}{n} \sum_{i=1}^{n} \delta x_{i}(x)\]

那么当采样足够多的时候，经验分布函数是可以逼近数据分布 \(p_{data}\) 的

那么问题就可以转化成，现在要训练一个生成模型 \(g_{\theta}\)，去优化 \(Distance(g_{\theta},\mu_{X})\) ，比起之前所说的比较抽象的拟合数据分布，这样就跟切实了

\(f-divergence\) 在 \(\mu_{X}(x)\) 下就产生了定义上的问题，因为 \(\mu_{X}\) 是一个离散的分布，\(supp(\mu_{X}) = \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}\) ，在此之外的部分无法去计算 \(Distance(g_{\theta},\mu_{X})\) ，这样的话就无法用来有效进行 SGD ，那么基于逼近 \(JS-divergence\) 的 vanilla-GAN 会出现难以训练的问题也是正常的了

在这样的背景下，去找一个能够有效计算 \(Distance(g_{\theta},\mu_{X})\) 的距离也就不奇怪了，\(Wasserstein\) 距离呼之欲出，关于 \(Wasserstein\) 距离的基础部分最优传输

有了合适的距离后，在这个框架下审视 \(Wasserstein \; GAN\)，通过 \(Wasserstein\) 距离来优化经验分布和生成分布间的距离： \(W_{p}(g_{\theta},\mu_{X}):=\left(\inf _{\gamma \in \Gamma(g_{\theta},\mu_{X})} \int_{X \times X} d(x, y)^{p} \mathrm{~d} \gamma(x, y)\right)^{1 / p}\)

但是这样的话，由于要优化的参数 \(\theta\) 出现在了 constraint 上，会对求解梯度造成影响，考虑对偶问题：

进一步取 \(p=1\) ，有 \(Kantorvich-Rubinstein \; Duality\)：

\[W_{p}(g_{\theta},\mu_{X}):= \sup _{|\mid f \|_{L} \leq 1}[\underset{x \sim g_{\theta}}{\mathbb{E}}[f(x)]-\underset{y \sim \mu_{X}}{\mathbb{E}}[f(y)]]\]

这样约束变成了在满足 \(\| f \|_{L} \leq 1\) 的函数中取康托罗维奇势能 \(\tilde{f}\) 即可

但是真正应用的时候，每次都完整计算一次 \(Wasserstein\) 距离，这样计算量会爆炸的，因此训练一个以 \(w\) 为参数的 \(f_{w}\) 的神经网络作为 \(Wasserstein\) 距离的估计，为了限制 \(f_{w}\) 在 \(\| f \|_{L} \leq 1\) 中，采用weight clip技巧

整理一下 \(Wasserstein \; GAN\) 的训练过程，可以总结出这样的loss function：

\[\min_{\theta}\max _{w \in \mathcal{W}} \mathbb{E}_{x \sim \mathbb{P}_{r}}\left[f_{w}(x)\right]-\mathbb{E}_{z \sim p(z)}\left[f_{w}\left(g_{\theta}(z)\right]\right.\]

那么有两件事情值得一提：

看起来和 vanilla-GAN 的 loss function 有异曲同工之妙：
\[\min _{G} \max _{D} V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\mathrm{data}}(\boldsymbol{x})}[f(D(\boldsymbol{x}))]+\mathbb{E}_{\mathbf{z} \sim p_{\boldsymbol{z}}(\mathbf{z})}[f(1-D(G(\mathbf{z}))]\]
没错，这一类设计优化函数的思想，也被总结为 IPM （Integral Probability Metric）
\(Wasserstein \; GAN\) 的一个核心思想就是利用对偶问题，把 \(\theta\) 从约束中化去，那么是否有在取别的 \(p\) 的情况下，是否有别的对偶呢？有的，比如 Sobelev GAN 就利用 \(p=2\) 的情况来设计算法：

\[\sup _{f \in W^{1,2}(\mathcal{X}, \mu)} \mathbb{E}_{x \sim \mathbb{g_{\theta}}} f(x)-\mathbb{E}_{x \sim \mathbb{\mu_X}} f(x) \quad W^{1,2}(\mathcal{X}, \mu)=\left\{f: \mathcal{X} \rightarrow \mathbb{R}, \int_{\mathcal{X}}\left\|\nabla_{x} f(x)\right\|^{2} \mu(x) d x<\infty\right\}\]

Variational autoencoder

Vanilla-VAE

关于 VAE 的基础部分，可以看这一部分中关于 VAE的介绍，现在开始从直觉上仿照 autoencoder 的结构来构造 VAE：

\[\begin{array}{l} \phi: \mathcal{X} \rightarrow \mathcal{F} \\ \psi: \mathcal{F} \rightarrow \mathcal{X} \\ \phi, \psi=\underset{\phi, \psi}{\arg \min }\|X-(\psi \circ \phi) X\|^{2} \end{array}\]

类似的，在 VAE 中也有两个对应的耦合分布，生成分布（解码器）\(p_{\theta}(x\mid z)\) 和推断分布（编码器）\(q_{\phi}(z\mid x)\)，那么问题变成了如何用这两个分布构造分布之间的复建误差：

首先想到的是能在 VAE 框架下把 \(p(x)\) 表达出来，然后用 \(Wasserstein\) 距离做和经验分布的比较嘛？可惜即使是 VAE，一样做不到这样的效果，依然受制于 intractability:

\[p(x)=\int p_{\theta}(x \mid z) p_{z}(z) d z = \sum_1^n p_{\theta}(x \mid z_i) p_{z}(z_i)\]

但是上式中 \(\int p_{\theta}(x \mid z) p_{z}(z) d z\)，启发我们是否能用推断分布 \(q_{\phi}(z\mid x)\) 作为 \(p_{z}(z)\) 的替代呢？这样某种意义上也体现了复建的过程，可能 \(Evidence \; Lower \; Bound\) 就是受此启发的：

\[\begin{aligned} \log p_{\boldsymbol{\theta}}(\mathbf{x}) &=\mathbb{E}_{q_{\phi}(\mathbf{z} \mid \mathbf{x})}\left[\log p_{\boldsymbol{\theta}}(\mathbf{x})\right] \\ &=\mathbb{E}_{q_{\phi}(\mathbf{z} \mid \mathbf{x})}\left[\log \left[\frac{p_{\boldsymbol{\theta}}(\mathbf{x}, \mathbf{z})}{p_{\boldsymbol{\theta}}(\mathbf{z} \mid \mathbf{x})}\right]\right] \\ &=\mathbb{E}_{q_{\phi}(\mathbf{z} \mid \mathbf{x})}\left[\log \left[\frac{p_{\boldsymbol{\theta}}(\mathbf{x}, \mathbf{z})}{q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})} \frac{q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})}{p_{\boldsymbol{\theta}}(\mathbf{z} \mid \mathbf{x})}\right]\right] \\ &= \mathbb{E}_{q_{\phi}(\mathbf{z} \mid \mathbf{x})}\left[\log \left[\frac{p_{\boldsymbol{\theta}}(\mathbf{x}, \mathbf{z})}{q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})} \frac{q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})}{p_{\boldsymbol{\theta}}(\mathbf{z} \mid \mathbf{x})}\right]\right] \\ &= \underbrace{\mathbb{E}_{q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})}\left[\log \left[\frac{p_{\boldsymbol{\theta}}(\mathbf{x}, \mathbf{z})}{q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})}\right]\right]}_{=\mathcal{L}_{\boldsymbol{\theta}, \boldsymbol{\phi}}(\mathbf{x})\\(\mathrm{ELBO})} + \underbrace{\mathbb{E}_{q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})}\left[\log \left[\frac{q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})}{p_{\boldsymbol{\theta}}(\mathbf{z} \mid \mathbf{x})}\right]\right]}_{=D_{K L}\left(q_{\phi}(\mathbf{z} \mid \mathbf{x}) \| p_{\boldsymbol{\theta}}(\mathbf{z} \mid \mathbf{x})\right)} \end{aligned}\]

这一部分还是利用 MLE 的思想去做 \(\theta,\phi\) 的优化，后面会给出一个不甚严谨证明：MLE 与 \(\min_{\theta,\phi}Distance\) 是等价的

把上式中的第一部分取出来，我们得到了一个 \(\log p_{\theta}(\mathbf{x})\) 的下界，同时还可以进一步拆解：

\[\begin{aligned} \mathrm{L}_{\theta, \phi}(\boldsymbol{x}) &=\mathbb{E}_{\mathrm{q}_{\phi}(z \mid x)}\left[\log p_{\theta}(\boldsymbol{x} \mid \boldsymbol{z})+\log p_{\theta}(\boldsymbol{z})-\log \mathrm{q}_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})\right] \\ &=\mathbb{E}_{q_{\phi}(z \mid x)}\left[\log p_{\theta}(x \mid z)\right]-D_{K L}\left[q_{\phi}(z \mid x) \| p_{\theta}(z)\right] \end{aligned}\]

上式中第一部分代表复建的误差，由推断分布编码成 \(z\) 的 \(x\) 与最后生成分布解码的 \(x\) 的误差越小，第一项越大，而第二部分控制最后用来抽样的 \(p_{z}(z)\) 于推断分布 \(q_{\phi}(z \mid x)\) 相差不远

Wasserstein VAE

那么还是尝试用用生成分布去拟合经验分布这个角度来看 VAE 的过程，比起 GAN 去看映射到数据空间 \(X\) 的 \(g_{\theta}(z)\) 有多可能在数据流形附近，VAE 是通过衡量数据分布整体做的，因此生成分布的部分从 \(\mathcal{Z}\) 考虑即可，改写最优传输问题为：

\[E(\theta)=\min _{\pi \in \mathcal{P}(Z \times \mathcal{X})}\left\{\int_{\mathcal{Z} \times \mathcal{X}} c\left(g_{\theta}(z), y\right) \mathrm{d} \pi(z, y) ; P_{1 \#} \pi= p_{\theta}, P_{2 \#} \pi=\mu_{X}\right\}\]

编码分布 \(q_{\phi} = P_{1 \#} \pi\)，在约束中要等于 \(p_{\theta}\)，这一点在实用中很难达到，弱化成正则项写入优化目标：

\[E_{\lambda}(\theta)=\min _{\pi}\left\{\int_{\mathcal{Z} \times \mathcal{X}} c\left(g_{\theta}(z), y\right) \mathrm{d} \pi(z, y)+\lambda D\left(P_{1 \#} \pi \mid p_{\theta}\right) ; P_{2 \#} \pi=\mu_{X}\right\}\]

而第一项是从拟合一个分布的角度去优化生成分布和经验分布间的距离的

An informal proof of Equivalent

两个视角（MLE 和 \(\min Distance(\mu \| \nu)\)）实际上做的事情是等价的

\[\begin{aligned} \tilde{\mu}_{X}(x)&=\frac{1}{n} \sum_{i=1}^{n} N\left(x_{i}, \sigma_{i}^{2}\right) \\ &\downarrow \lim _{\sigma_{i} \rightarrow 0}\tilde{\mu}_{X} \rightarrow \mu_{X} \\ \arg \max _{\theta} p_{\theta}(x) &\cong \arg \max_{\theta} \log p_{\theta}(x) \\ \log p_{\theta}(x) & = E_{\tilde{\mu}_{X}}\left[\log p_{\theta}(x)\right] =E_{\tilde{\mu}_{X}}\left[\log \frac{p_{\theta}(x)}{\tilde{\mu}_{X}(x)} \cdot \tilde{\mu}_{X}(x)\right] \\ & =-D_{KL}\left[\tilde{\mu}_{X} \| p_{\theta}\right]+H\left[\tilde{\mu}_{x}\right] \end{aligned}\]

因此优化经验分布和生成分布之间的距离是等价于 MLE 的

Generative Model Part 1:Intuition on Generative Model