• Optimal Transport Note: Part 2
  • Kantorovich Duality
    • Kantorovich Duality
      • Theorem 3.1. Kantorovich Duality
    • Fenchel-Rockafeller Duality
      • Theorem 3.2. Fenchel-Rockafellar Duality
      • Lemma 3.3
      • Theorem 3.4. Hahn-Banach Theorem（分离定理）
      • Proof of Fenchel-Rockafellar Duality
    • Proof of Kantorovich Duality
  • Reference

Optimal Transport Note: Part 2

Kantorovich Duality

自然的，康托洛维奇最优的离散形式是一个标准的线性规划中的运输问题，那么很自然的，联想到应当可以定义康托洛维奇形式的对偶形式

Kantorovich Duality

Theorem 3.1. Kantorovich Duality

有 Polish space 和其上的测度 \((X, \mu)\) 和 \((Y, \nu)\) ，有传输代价函数 \(c: X \times Y \rightarrow[0,+\infty]\) 是 lower semi continuous的函数

类似之前的定义康托洛维奇传输代价 \(\mathbb{K}(\pi)\) ，在此之外再定义一个康托洛维奇对偶传输代价 \(\mathbb{J}(\varphi, \psi)\) 与相应空间 \((\varphi, \psi) \in \Phi_{c}\)：

\[\mathbb{J}: L^{1}(\mu) \times L^{1}(\nu) \rightarrow \mathbb{R}, \quad \mathbb{J}(\varphi, \psi)=\int_{X} \varphi \mathrm{d} \mu+\int_{Y} \psi \mathrm{d} \nu \\ \Phi_{c}=\left\{(\varphi, \psi) \in L^{1}(\mu) \times L^{1}(\nu): \varphi(x)+\psi(y) \leq c(x, y)\right\}\]

有 \(\mu \text { -almost } x \in X\) 且 \(\nu \text { -almost } y \in Y\) 成立的不等式：

\[\min _{\pi \in \Pi(\mu, \nu)} \mathbb{K}(\pi)=\sup _{(\varphi, \psi) \in \Phi_{c}} \mathbb{J}(\varphi, \psi)\]

此为康托洛维奇对偶性的定义，若套用一个具体场景的话，不妨用 \(shippers \; problem\) 的例子

煤矿主可以选择自己从矿 \(x\) 运输到工厂 \(y\)，这样所付出的的运输代价为 \(c(x,y)\) ，船主提出比起矿主自己运，可以由他来运，仅需要在起点和终点付出一笔装船费和卸货费为 \(\varphi(x),\psi(y)\)，当然为了使方案有说服力，显然几乎处处 \(\varphi(x)+\psi(y) \leq c(x, y)\) ，才能够使得矿主接受方案。那么康托洛维奇对偶性就是在说：最优传输代价应当等于由他人来运的成本价，下面在比较强的条件下给出证明：

设康托洛维奇最优传输代价 \(M = \inf _{\pi \in \Pi(\mu, \nu)} \mathbb{K}(\pi)\)，也可以进一步写成：

\[M=\inf _{\pi \in \mathcal{M}_{+}(X \times Y)} \sup _{(\varphi, \psi)}\left(\int_{X \times Y} c(x, y) \mathrm{d} \pi+\int_{X} \varphi \mathrm{d}\left(\mu-P_{\#}^{X} \pi\right)+\int_{Y} \psi \mathrm{d}\left(\nu-P_{\#}^{Y} \pi\right)\right)\]

由于 \((\varphi, \psi) \in C_{b}^{0}(X) \times C_{b}^{0}(Y)\)，则对于函数 \(\sup _{\varphi \in C_{b}^{0}(X)} \int_{X} \varphi \mathrm{d}\left(\mu-P_{\#}^{X} \pi\right)\) 有性质：

\[\sup _{\varphi \in C_{b}^{0}(X)} \int_{X} \varphi \mathrm{d}\left(\mu-P_{\#}^{X} \pi\right)=\left\{\begin{array}{ll} +\infty & \text { if } \mu \neq P_{\#}^{X} \pi \\ 0 & \text { else. } \end{array}\right.\]

因此为了取到下界，\(\mu,\nu\) 被限制在 \(P_{\#}^{X} \pi=\mu\) 和 \(P_{\#}^{X} \pi=\mu\) 上，即 \(\pi \in \Pi(\mu, \nu)\)，若假设 \(MiniMax=MaxMini\)，进一步整理则有：

\[M=\sup _{(\varphi, \psi)}\left(\int_{X} \varphi \mathrm{d} \mu+\int_{Y} \psi \mathrm{d} \nu+\inf _{\pi \in \mathcal{M}_{+}(X \times Y)} \int_{X \times Y} c(x, y)-\varphi(x)-\psi(y) \mathrm{d} \pi\right)\]

当 \(\varphi(x)+\psi(y) \leq c(x, y)\) 处处成立时，可以知道当 \((\varphi, \psi) \in \Phi_{c}\)，取 \(\pi \equiv 0 \in \mathcal{M}_{+}(X \times Y)\) 就可以使

\[\inf _{\pi \in \mathcal{M}_{+}(X \times Y)} \int_{X \times Y} c(x, y)-\varphi(x)-\psi(y) \mathrm{d} \pi=0\]

则有康托洛维奇对偶性成立：

\[\inf _{\pi \in \Pi(\mu, \nu)} \mathbb{K}(\pi)=\sup _{(\varphi, \psi) \in \Phi_{c}} \int_{X} \varphi(x) \mathrm{d} \mu(x)+\int_{Y} \psi(y) \mathrm{d} \nu(y)\]

Fenchel-Rockafeller Duality

之前在证明中用到的 Minimax Principle，即 \(sup \; inf = inf \; sup\)，这在凸函数时才成立，下面给出一些与凸函数相关的结果

赋范线性空间 \(E\) 上有凸函数 \(\Theta: E \rightarrow \mathbb{R} \cup\{+\infty\}\)，其勒让德变换定义为：

\[\Theta^{*}\left(z^{*}\right)=\sup _{z \in E}\left(\left\langle z^{*}, z\right\rangle-\Theta(z)\right)\]

勒让德变换的低维形式，可以理解变换到导数，及其对应的 \(y\) 轴截距：

\(\quad \quad \quad \quad (x, f(x)) \stackrel{\text { Lengendre }}{\longrightarrow}\left(p, f^{*}(p)\right) \quad \quad \quad \quad \quad\)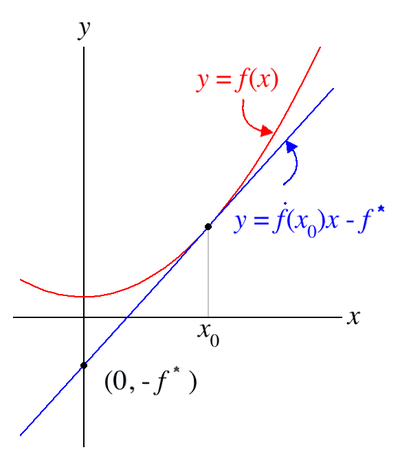

Theorem 3.2. Fenchel-Rockafellar Duality

利用勒让德变换，可以定义 Fenchel-Rockafellar 对偶

赋范线性空间 \(E\) 上有凸函数 \(\Theta , \Xi : E \rightarrow \mathbb{R} \cup\{+\infty\}\)，若存在 \(z_{0} \in E,s.t \; \Theta\left(z_{0}\right)<\infty, \Xi\left(z_{0}\right)<\infty\) 且 \(\Theta\) 在 \(z_{0}\)，则： \(\inf _{E}(\Theta+\Xi)=\max _{z^{*} \in E^{*}}\left(-\Theta^{*}\left(-z^{*}\right)-\Xi^{*}\left(z^{*}\right)\right) .\)

Lemma 3.3

假设赋范线性空间 \(E\)：

1. 有凸函数 \(\Theta: E \rightarrow \mathbb{R} \cup\{+\infty\}\)，定义 \(epigraph \; A\) 也是凸的 \(A=\{(z, t) \in E \times \mathbb{R}: t \geq \Theta(z)\}\)

2. 有凹函数 \(\Theta: E \rightarrow \mathbb{R} \cup\{+\infty\}\)，定义 \(hypograph \; A\) 也是凹的 \(B=\{(z, t) \in E \times \mathbb{R}: t \leq \Theta(z)\}\)

3. \(C \subset E\) 是凸集，则 \(C\) 的内点 \(\operatorname{int}(C)\) 是凸的

4. \(D \subset E\) 是凸集且 \(int(C) \neq \emptyset\) ，则 \(\bar{D}=\overline{\operatorname{int}(D)}\)

Theorem 3.4. Hahn-Banach Theorem（分离定理）

\(E\) 是拓扑向量空间，有非空，不相交，凸子集 \(A, B \subset E\) ，且有 \(A\) 是开集，则存在一个分离超平面分开 \(A, B\)

Proof of Fenchel-Rockafellar Duality

通过勒让德变换可以写出：

\[-\Theta^{*}\left(-z^{*}\right)-\Xi^{*}\left(z^{*}\right)=\inf _{x, y \in E}\left(\Theta(x)+\Xi(y)+\left\langle z^{*}, x-y\right\rangle\right)\]

选择 \(y=x\) 则有：

\[\inf _{x \in E}(\Theta(x)+\Xi(x)) \geq \sup _{z^{*} \in E^{*}}\left(-\Theta^{*}\left(-z^{*}\right)-\Xi^{*}\left(z^{*}\right)\right)\]

设 \(M=\inf (\Theta+\Xi)\) ，这里证明完成了一半，下证 \(\sup _{z^{*} \in E^{*}}\left(-\Theta^{*}\left(-z^{*}\right)-\Xi^{*}\left(z^{*}\right)\right) \geq M\)

设集合 \(A, B\)，且由引理知 \(A, B\) 是凸的

\[\begin{array}{l} A=\{(x, \lambda) \in E \times \mathbb{R}: \lambda \geq \Theta(x)\} \\ B=\{(y, \sigma) \in E \times \mathbb{R}: \sigma \leq M-\Xi(y)\} . \end{array}\]

定义 \(C=\operatorname{int}(A)\) ，由引理知 \(C\) 也是凸的，且由于 \(C=\operatorname{int}(A)\)，知对于 \((x, \lambda) \in C\)

\[\lambda>\Theta(x) \Rightarrow \lambda+\Xi(x)>\Theta(x)+\Xi(x) \geq M\]

因此 \(B,C\) 不相交，且知 \(B,C\) 是凸的，非空的，由分离定理知存在超平面 \(\Phi(x, \lambda)=f(x)+k \lambda （linear \;f）\)分离 \(B,C\)

\[\begin{aligned} \forall(x, \lambda) & \in C, & & f(x)+k \lambda \geq \alpha \\ \forall(x, \lambda) & \in B, & & f(x)+k \lambda \leq \alpha \end{aligned}\]

进一步的构造点列 \(\left(x_{n}, \lambda_{n}\right) \in C\) 逼近 \((x, \lambda) \in C\) ，\(\left(x_{n}, \lambda_{n}\right) \rightarrow(x, \lambda)\)，因此可知 \(f(x)+k \lambda \leftarrow f\left(x_{n}\right)+k \lambda_{n} \geq \alpha\) ，即：

\[\begin{array}{ll} \forall(x, \lambda) \in A, & f(x)+k \lambda \geq \alpha \\ \forall(x, \lambda) \in B, & f(x)+k \lambda \leq \alpha \end{array}\]

当取一个 \(\left(z_{0}, \lambda\right) \in A\) 当 \(\lambda\) 充分大时，可知 \(k \geq 0\)

下证 \(k>0\)，利用反证法，当 \(k=0\)，有

\[\begin{aligned} \forall(x, \lambda) \in A, & f(x) \geq \alpha & \Longrightarrow & f(x) \geq \alpha & \forall x \in \operatorname{Dom}(\Theta) \\ \forall(x, \lambda) \in B, & f(x) \leq \alpha & \Longrightarrow & f(x) \leq \alpha & \forall x \in \operatorname{Dom}(\Xi) . \end{aligned}\]

若有一个 \(z_{0}\)，有 \(\operatorname{Dom}(\Xi) \ni z_{0} \in \operatorname{Dom}(\Theta)\)，则 \(f\left(z_{0}\right)=\alpha\)，由 \(\Theta\) 的连续性就可以取一个邻域 \(B\left(z_{0}, r\right) \subset \operatorname{Dom}(\Theta)\)，在其中的点 \(z_{0}+\delta z\) ，\(\| z \|<r，|\delta|<1\) 满足：

\[f\left(z_{0}+\delta z\right) \geq \alpha \quad \Longrightarrow \quad f\left(z_{0}\right)+\delta f(z) \geq \alpha \quad \Longrightarrow \quad \delta f(z) \geq 0\]

由于对于 \(\delta \in(-1,1)\)都满足，因此 \(f(z)=0 \text ， z \in B(0, r)\)，那么如此一样的在 \(E\) 上取满足的点，就有 \(f \equiv 0 \text { on } E\)，这会导致无意义的超平面，因此 \(k > 0\)

于是对于 \((z, \Theta(z)) \in A\) 有：

\[\begin{aligned} \Theta^{*}\left(-\frac{f}{k}\right) &=\sup _{z \in E}\left(-\frac{f(z)}{k}-\Theta(z)\right) \\ &=-\frac{1}{k} \inf _{z \in E}(f(z)+k \Theta(z)) \\ & \leq-\frac{\alpha}{k} \end{aligned}\]

同时对 \((z, M-\Xi(z)) \in B\) 有：

\[\begin{aligned} \Xi^{*}\left(\frac{f}{k}\right) &=\sup _{z \in E}\left(\frac{f(z)}{k}-\Xi(z)\right) \\ &=-M+\frac{1}{k} \sup _{z \in E}(f(z)+k(M-\Xi(z))) \\ & \leq-M+\frac{\alpha}{k} \end{aligned}\]

这可以导出不等式的另一半：

\[M \geq \sup _{z^{*} \in E^{*}}\left(-\Theta^{*}\left(-z^{*}\right)-\Xi^{*}\left(z^{*}\right)\right) \geq-\Theta^{*}\left(-\frac{f}{k}\right)-\Xi^{*}\left(\frac{f}{k}\right) \geq \frac{\alpha}{k}+M-\frac{\alpha}{k}=M\]

于是 Fenchel-Rockafellar 对偶得证，在 \(z^{*}=\frac{f}{k}\) 取最大值时：

\[\inf _{x \in E}(\Theta(x)+\Xi(x))=M=\sup _{z^{*} \in E^{*}}\left(-\Theta^{*}\left(-z^{*}\right)-\Xi^{*}\left(z^{*}\right)\right)\]

Proof of Kantorovich Duality

康托洛维奇对偶性的证明分成两部分

1. 对于 \(\sup _{(\varphi, \psi) \in \Phi_{c}} J(\varphi, \psi) \leq \inf _{\pi \in \Pi(\mu, \nu)} \mathbb{K}(\pi)\)，这部分在 \(p\)-almost 意义下证明即可：

   对于 \((\varphi, \psi) \in \Phi_{C}\)，\(\pi \in \Pi(\mu, \nu)\)，取 \(A \subset X ， B \subset Y \; s.t \; \mu(A)=1,\nu(B)=1\)，以及代价不等式成立： \(\varphi(x)+\psi(y) \leq c(x, y) \quad \forall(x, y) \in A \times B\) 有 \(\pi\left(A^{c} \times B^{c}\right) \leq \pi\left(A^{c} \times Y\right)+\pi\left(X \times B^{c}\right)=\mu\left(A^{c}\right)+\nu\left(B^{c}\right)=0\)，进一步有： \(\begin{aligned} \pi(A \times B) &=\pi(X \times B)-\pi\left(A^{c} \times B\right) \\ &=\nu(B)-\pi\left(A^{c} \times Y\right)+\pi\left(A^{c} \times B^{c}\right) \\ &=1-\mu\left(A^{c}\right)+\pi\left(A^{c} \times B^{c}\right) \\ &=1 \end{aligned}\) 于是代价不等式在 \(\pi-\text { almost } (x, y)\) 成立： \(\mathbb{J}(\varphi, \psi)=\int_{X} \varphi \mathrm{d} \mu+\int_{Y} \psi \mathrm{d} \nu=\int_{X \times Y} \varphi(x)+\psi(y) \mathrm{d} \pi(x, y) \leq \int_{X \times Y} c(x, y) \mathrm{d} \pi(x, y)\)

2. 另一半证明在 \(X, Y\) 是紧集， \(c\) 连续的条件下证明：

   \(E=C_{b}^{0}(X \times Y)\) 有非负测度，于是有对偶空间 \(E^{*}=\mathcal{M}(X \times Y)\)，在 \(E\) 上定义：

   \[\begin{array}{l} \Theta(u)=\left\{\begin{array}{ll} 0 & \text { if } u(x, y) \geq-c(x, y) \\ +\infty & \text { else } \end{array}\right. \\ \Xi(u)=\left\{\begin{array}{ll} \int_{X} \varphi(x) \mathrm{d} \mu(x)+\int_{Y} \psi(y) \mathrm{d} \nu(y) & \text { if } u(x, y)=\varphi(x)+\psi(y) \\ +\infty & \text { else. } \end{array}\right. \end{array}\]

   可以证明 \(\Theta,\Xi\) 是凸的，取 \(u, v\) 满足 \(\Theta(u), \Theta(v)<+\infty\)，于是有 \(u(x, y) \geq-c(x, y)\)，\(v(x, y) \geq-c(x, y)\)

   \[t u(x, y)+(1-t) v(x, y) \geq c(x, y) \forall t \in [0,1] \\ \Downarrow \\ \Theta(t u+(1-t) v)=0=t \Theta(u)+(1-t) \Theta(v)\]

   因此 \(\Theta\) 是凸的，对于 \(\Xi\)，设 \(u(x, y)=\varphi_{1}(x)+\psi_{1}(y), v(x, y)=\varphi_{2}(x)+\psi_{2}(y)\)，则有：

   \[\Xi(t u+(1-t) v)=\int_{X} t \varphi_{1}+(1-t) \varphi_{2} \mathrm{~d} \mu+\int_{Y} t \psi_{1}+(1-t) \psi_{2} \mathrm{~d} \nu=t \Xi(u)+(1-t) \Xi(v)\]

   因此 \(\Xi\) 也是凸的，因此有 Fenchel-Rockafellar 对偶性成立：

   \[\inf _{u \in E}(\Theta(u)+\Xi(u))=\max _{\pi \in E^{*}}\left(-\Theta^{*}(-\pi)-\Xi^{*}(\pi)\right)\]

   对于左半部分 \(\inf _{u \in E}(\Theta(u)+\Xi(u))\)，可知：

   \[\inf _{u \in E}(\Theta(u)+\Xi(u)) \geq \inf _{\varphi(x)+\psi(y) \geq-c(x, y) \\ \varphi \in L^{1}(\mu), \psi \in L^{\prime}(\nu)} \int_{X} \varphi(x) \mathrm{d} \mu(x) =-\sup _{(\varphi, \psi) \in \Phi_{c}} \mathbb{J}(\varphi, \psi)\]

   而对于右半部分 \(\max _{\pi \in E^{*}}\left(-\Theta^{*}(-\pi)-\Xi^{*}(\pi)\right)\)，代入勒让德变换的定义知：

   \[\Theta^{*}(-\pi)=\sup _{u \in E}\left(-\int_{X \times Y} u \mathrm{~d} \pi-\Theta(u)\right)=\sup _{u \geq-c}-\int_{X \times Y} u \mathrm{~d} \pi=\sup _{u \leq c} \int_{X \times Y} u \mathrm{~d} \pi\]

   即 \(\Theta\) 的对偶：

   \[\Theta^{*}(-\pi)=\left\{\begin{array}{ll} \int_{X \times Y} c(x, y) \mathrm{d} \pi & \text { if } \pi \in \mathcal{M}_{+}(X \times Y) \\ +\infty & \text { else. } \end{array}\right.\]

   对于 \(\Xi^{*}\) 有：

   \[\begin{equation} \begin{aligned} \Xi^{*}(\pi) &=\sup _{u \in E}\left(\int_{X \times Y} u \mathrm{~d} \pi-\Xi(u)\right) \\ &=\sup _{u(x, y)=\varphi(x)+\psi(y)}\left(\int_{X \times Y} u \mathrm{~d} \pi-\int_{X} \varphi(x) \mathrm{d} \mu-\int_{Y} \psi(y) \mathrm{d} \nu\right) \\ &=\sup _{u(x, y)=\varphi(x)+\psi(y)} \left( \int_{X} \varphi \mathrm{d}\left(P_{\#}^{X}-\mu\right)+\int_{Y} \psi \mathrm{d}\left(P_{\#}^{Y}-\nu\right)\right) \\ &=\left\{\begin{array}{ll} 0 & \text { if } \pi \in \Pi(\mu, \nu) \\ +\infty & \text { else. } \end{array}\right. \end{aligned} \end{equation}\]

   则右半部分 \(\max _{\pi \in E^{*}}\left(-\Theta^{*}(-\pi)-\Xi^{*}(\pi)\right)\) 等于：

   \[\max _{\pi \in E^{*}}\left(-\Theta^{*}(-\pi)-\Xi^{*}(\pi)\right) = - \int_{X \times Y} c(x, y) \mathrm{d} \pi = - \min _{\pi \in \Pi(\mu, \nu)} \mathbb{K}(\pi)\]

   因此康托洛维奇对偶性在 \(X, Y\) 是紧集， \(c\) 连续的条件下得证：

   \[\inf _{\pi \in \Pi(\mu, \nu)} \mathbb{K}(\pi)=\sup _{(\varphi, \psi) \in \Phi_{c}} \int_{X} \varphi(x) \mathrm{d} \mu(x)+\int_{Y} \psi(y) \mathrm{d} \nu(y)\]

Reference

1. Matthew Thorpe “Introduction to Optimal Transportation”