Optimal Transport Note: Part 1
Formulation of Optimal Transport
Monge Formulation
最优传输的背景是蒙日考虑在建造防御工事时,如何花费最少的劳动力去把四散的土堆运输到其他处的防御工事处,在此之上抽象出了最优传输问题,最优传输问题总共有两种提法,蒙日形式(Monge Formulation)和康托洛维奇形式(Kantorovich Formulation),康托洛维奇形式更加完善,更加适合理论研究,蒙日形式则更加适合应用上的计算。
先给出蒙日形式的最优传输问题:
有概率空间 \((X, \Sigma_X , \mu)\) 和 \((Y, \Sigma_Y , \nu)\)
定义代价函数 \(c: X \times Y \rightarrow[0,+\infty]\),测量运输 \(x \in X\) 到 \(y \in Y\) 的代价
定义传输映射 \(T: X \rightarrow Y\) 将 \(\mu \in \mathcal{P}(X)\) 传输到 \(\nu \in \mathcal{P}(Y)\),当
\[\nu(B)=\mu\left(T^{-1}(B)\right) \quad \forall \; \nu \text { -measurable } B\]这样定义保证了传输映射必须双射,而测度不变,直观上来说,就是传输映射 \(T\),从 \(X\) 中取走多少土,就相应有多少土运到 \(Y\) 中,如下图所示
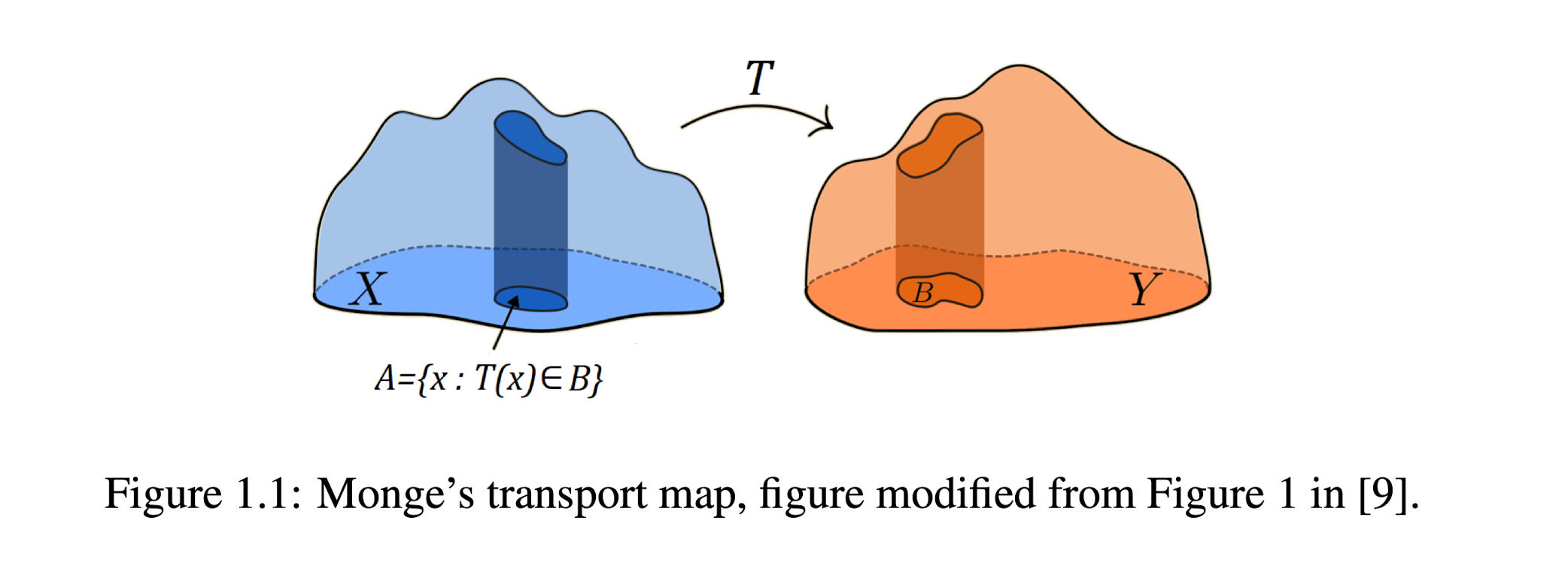
在上面的定义下,称 \(T\) 传输 \(\mu\) 到 \(\nu\) ,记 \(\nu=T_{\#} \mu\)
然后对于传输映射就有两条性质:
对于 \(\mu \in \mathcal{P}(X), T: X \rightarrow Y, S: Y \rightarrow Z\),以及 \(f \in L^{1}(Y)\)
-
变量变换公式:分别在原像集和像集的角度下,(\(f \equiv 1\) 则为上面的质量不变,推广质量不变到期望不变?)
\[\int_{Y} f(y) \mathrm{d}\left(T_{\#} \mu\right)(y)=\int_{X} f(T(x)) \mathrm{d} \mu(x)\] -
映射复合公式:推广到存在中转站这样的情况下而定义
\[(S \circ T)_{\#} \mu=S_{\#}\left(T_{\#} \mu\right)\]
上面的定义都很自然又严谨,但是很可惜,由于蒙日形式下要求传输映射 \(T\) 可逆,其不一定存在
比如在 \(x_{1}\) 处有 \(1\) 单位沙堆,而在 \(y_{1},y_{2}\) 处分别有两个 \(\frac{1}{2}\) 单位的防御工事要建造
换言之 \(\mu=\delta_{x_{1}}\) 而 \(\nu=\frac{1}{2} \delta_{y_{1}}+\frac{1}{2} \delta_{y_{2}}\) ,由于\(\nu\left(\left\{y_{1}\right\}\right)=\frac{1}{2}\),其不可能等于 \(\mu\left(T^{-1}\left(y_{1}\right)\right) \in\{0,1\}\),因此传输映射 \(T\) 不存在
对于上述的问题暂且不表,于是先定义蒙日形式的最优传输问题:\(T: X \rightarrow Y \text { subject to } \nu=T_{\#} \mu\)
\[\text { minimise } \mathbb{M}(T)=\int_{X} c(x, T(x)) \mathrm{d} \mu(x)\]Kantorovich Formulation
由于蒙日形式下,定义的最优传输 \(x \mapsto T(x)\) ,由于传输映射需要保证映射的特性,或者直观上来说, \(x_{1}\) 处的土堆不能分割,只能全部传输到另一个点 \(y_{1}\) 处,需要更加灵活的定义
因此康托洛维奇定义了传输计划 \(\pi \in \mathcal{P}(X \times Y)\) ,传输计划一样要服从传输质量不变性的约束,但在此之上,传输计划使得 \(x_{1}\) 处的土堆可以运输到多个目的地 \(\{y_{1},...,y_{n}\}\) 处,只需要满足 \(\mu({x_1})=\nu(\{y_{1},...,y_{n}\})\) 即可
或者考虑联合分布和边际分布的概念,在概率空间 \((X, \Sigma_X , \mu)\) 和 \((Y, \Sigma_Y , \nu)\) 的基础上,有\(\pi \in \mathcal{P}(X \times Y)\) ,记 \(\mathrm{d} \pi(x, y)\) 是从 \(x\) 传输到 \(y\) 的质量,服从
\[\pi(A \times Y)=\int_{A \times Y} d\pi\left(x,y\right)=\mu(A) \quad \pi(X \times B)=\int_{X \times B} d\pi\left(x,y\right)=\nu(B)\]记 \(\Pi(\mu, \nu)\) 为传输方案的集合,比起传输映射 \(T\) 可能不存在的问题,传输计划 \(\Pi(\mu, \nu)\) 永远非空,因为有一个平凡解 \(\pi^{*}\) ,取定 \(\{y^*\} \in \Sigma_{Y}\) ,对应的 \(X\) 上的起点在满足约束 \(\int_{X } d\pi\left(x,y^*\right)=\nu(y^*)\) 对 \(\nu(y^*)\) 成比例取值即可,如下图所示
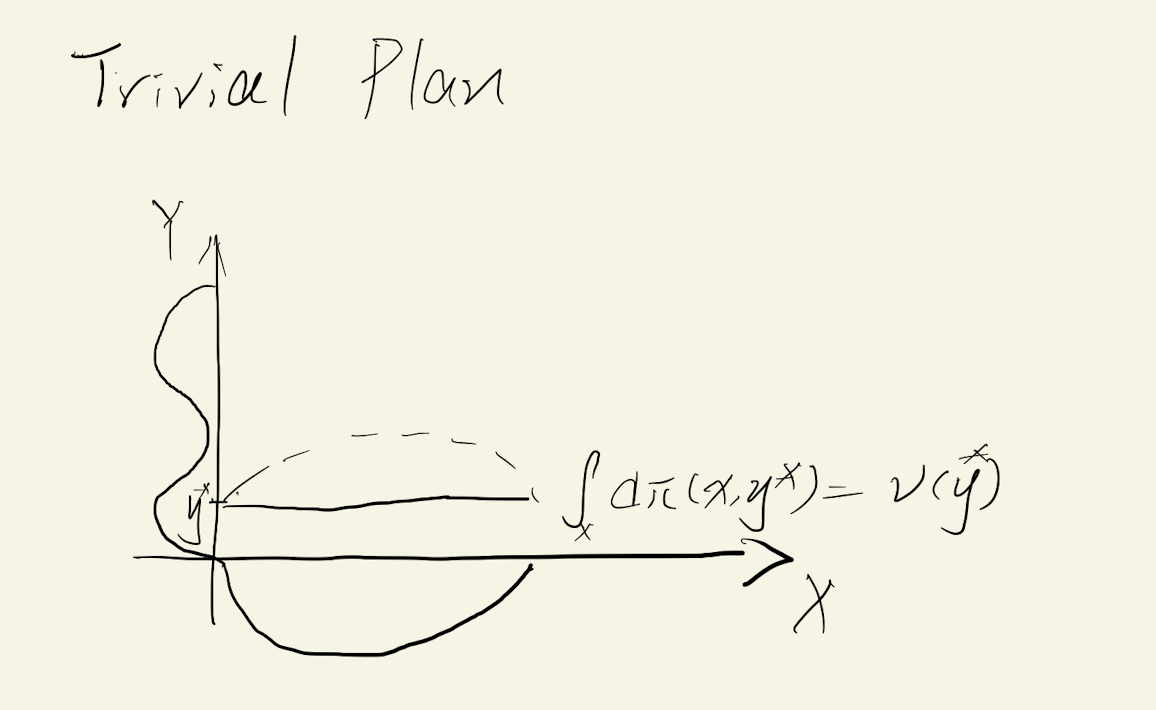
定义好了传输计划后,就可以定义康托洛维奇形式的最优传输问题:\(\mu \in \mathcal{P}(X) ,\nu \in \mathcal{P}(Y)\)
\[\text { minimise } \mathbb{K}(\pi)=\int_{\mathrm{X} \times Y} c(x, y) \mathrm{d} \pi(x, y) \quad \text{subject to} \quad \pi \in \Pi(\mu, \nu)\]下面证明蒙日形式与康托洛维奇形式的关系:假设蒙日形式最优存在,\(T^{\dagger}: X \rightarrow Y\),定义 \(d \pi(x, y)=\mathrm{d} \mu(x) \delta_{y=T^{\dagger}(x)}\)
\[\begin{array}{l} \pi(A \times Y)=\int_{A} \delta_{T^{\dagger}(x) \in Y} \mathrm{~d} \mu(x)=\mu(A) \\ \pi(X \times B)=\int_{X} \delta_{T^{\dagger}(x) \in B} \mathrm{~d} \mu(x)=\mu\left(\left(T^{\dagger}\right)^{-1}(B)\right)=T_{\#}^{\dagger} \mu(B)=\nu(B) \end{array}\]于是 \(\pi \in \Pi(\mu, \nu)\) ,
\[\int_{X \times Y} c(x, y) \mathrm{d} \pi(x, y)=\int_{X} \int_{Y} c(x, y) \delta_{y=T^{\dagger}(x)} \mathrm{d} y \mathrm{~d} \mu(x)=\int_{X} c\left(x, T^{\dagger}(x)\right) \mathrm{d} \mu(x)\]于是有
\[\inf \mathbb{K}(\pi) \leq \inf \mathbb{M}(T)\]而当传输计划与传输映射等价的时候,即 \(d \pi^{\dagger}(x, y)=\mathrm{d} \mu(x) \delta_{y=T^{\dagger}(x)}\) 时,此时有 \(\inf \mathbb{K}(\pi) = \inf \mathbb{M}(T)\) ,此时蒙日形式与康托洛维奇形式是等价的
最优传输的一个应用是,利用最优传输的插值:
\[\begin{aligned} \mu_{t}&=\left((1-t) \mathrm{Id}+t T^{\dagger}\right)_{\#} \mu \\ \mu_{0}(B)&=\left(\mathrm{Id}\right)_{\#} \mu(B)=\mu(\mathrm{Id}^{-1}(B))=\mu(B) \\ \mu_{1}(B)&=\mu_{1}\left(T^{\dagger-1}(B)\right)=\nu(B) \end{aligned}\]其效果会比单纯的在欧氏空间中插值:
\[\mu_{t}^{E}=(1-t) \mu+t \nu\]在可视化后的效果上更好一些:
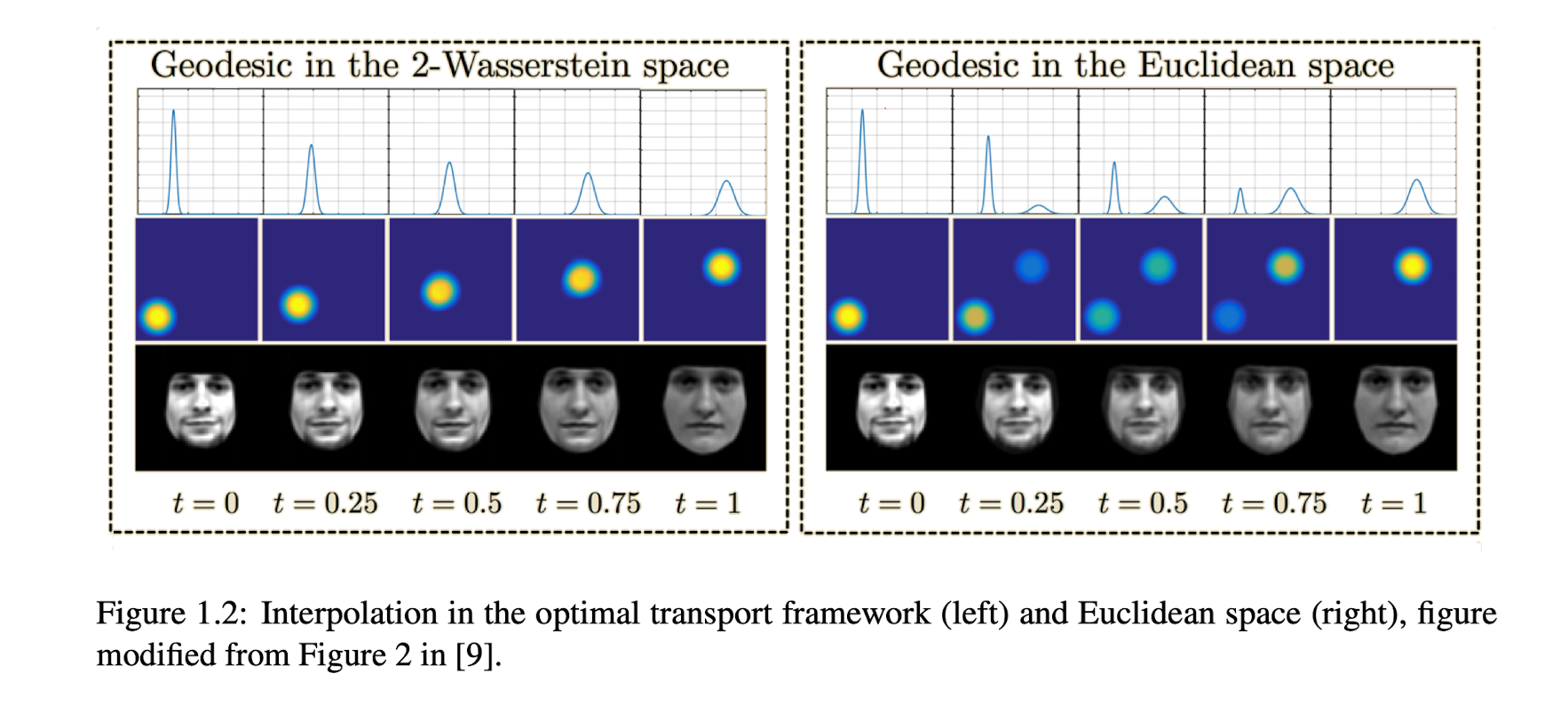
Special Cases
一般意义下的最优传输问题,还需要康托洛维奇对偶性等工具,但是在此之前,有两种特殊的情况,不用对偶性就可以解决,于是先摘了这些“低垂的果实” X:)
Optimal Transport in One Dimension
在一维情况下,有概率空间 \((X, \Sigma_X , \mu)\) 和 \((Y, \Sigma_Y , \nu)\) 下,进而利用 \(\mu,\nu\) 可以定义右连续,不减的 \(c.d.f\) \(F(x),G(y)\) ,有性质:
\[F(x)=\int_{-\infty}^{x} \mathrm{~d} \mu=\mu((-\infty, x]) \\ F(-\infty)=0 \quad F(+\infty)=1 \\\]同时,可以定义广义逆 \(F^{-1}\)
\[F^{-1}(t)=\inf \{x \in \mathbb{R}: F(x)>t\} \\ F^{-1}(F(x)) \geq x \quad F\left(F^{-1}(t)\right) \geq t\]进一步当 \(F\) 可逆时
\[F^{-1}(F(x))=x \quad F\left(F^{-1}(t)\right)=t\]以上的定义,对于 \(\nu\) 来说,也是一样的再做一遍
然后就有了 Theorem 2.1
Theorem 2.1
\(\mu, \nu \in \mathcal{P}(\mathbb{R})\) 其 \(c.d.f\) 分别是 \(F,G\), 认为 \(c(x, y)=d(x-y)\) 是凸的且连续的,\(\pi^{\dagger} \in \mathcal{P}(\mathbb{R}^{2})\) 且有 \(c.d.f \quad H(x, y)=\min \{F(x), G(y)\}\) ,则 \(\pi^{\dagger} \in \Pi(\mu, \nu)\) 且 \(\pi^{\dagger}\) 是康托洛维奇形式最优传输问题的解,且在代价函数 \(c(x,y)\) 下的传输代价为
\[\min _{\pi \in \Pi(\mu, \nu)} \mathbb{K}(\pi)=\int_{0}^{1} d\left(F^{-1}(t)-G^{-1}(t)\right) \mathrm{d} t\]Corollary 2.2
-
当 \(c(x, y)= \lvert x-y \rvert\) ,则最优传输代价也等于两个 \(c.d.f\) 的 \(L^1\) 距离:
\[\inf _{\pi \in \Pi(\mu, \nu)} \mathbb{K}(\pi)=\int_{\mathbb{R}}|F(x)-G(x)| \mathrm{d}\]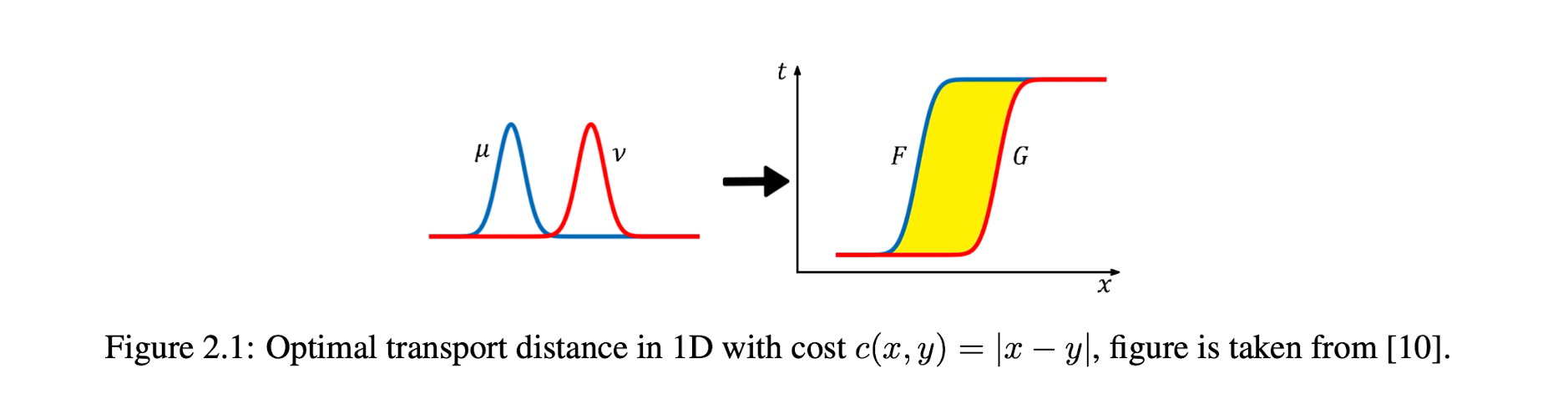
如图所示,描述积分区域可以用两种方法:
\[\begin{aligned} \mathcal{A} &=\left\{(x, t): \min \left\{F^{-1}(t), G^{-1}(t)\right\} \leq x \leq \max \left\{F^{-1}(t), G^{-1}(t)\right\}, t \in[0,1]\right\} \\ &= \{(x, t): \min \{F(x), G(x)\} \leq t \leq \max \{F(x), G(x)\}, x \in \mathbb{R}\} \end{aligned}\]且 \(\max \{a, b\}-\min \{a, b\}= \lvert a-b \rvert\) 即为代价函数即可证明
-
若传输计划等价于传输映射 \(\min _{\pi \in \Pi(\mu, \nu)} \mathbb{K}(\pi)=\min _{T: T_{\#} \mu=\nu} \mathbb{M}(T)\) ,则 \(T^{\dagger}=G^{-1} \circ F\) 是蒙日形式的最优传输映射:
\[\inf _{T: T_{\#} \mu=\nu} \mathbb{M }(T)=\mathbb{M}\left(T^{\dagger}\right)\]-
第一部分证明 \(T^{\dagger}_{\#} \mu=\nu\) :
利用之前的复合映射公式,知\(T^{\dagger}_{\#} \mu =G_{\#}^{-1}\left(F_{\#} \mu\right)\) ,由于 \(F\) 连续 ,\(\exists x_t,\forall t \in (0,1) ,F\left(x_{t}\right)=t\) ,于是对于 \(F_{\#} \mu\) 有:
\[\begin{aligned} F_{\#} \mu([0, t]) &=\mu(\{x: F(x) \leq t\}) \\ &=\mu\left(\left\{x: x \leq x_{t}\right\}\right) \\ &=F\left(x_{t}\right) \\ &=t \\ &\Rightarrow F_{\#} \mu=\mathcal{L}_{[0,1]} \end{aligned}\]于是问题变成证明 \(T^{\dagger}_{\#} \mu =G_{\#}^{-1}\left(\mathcal{L}_{[0,1]}\right)\)
\[\begin{aligned} G_{\#}^{-1} \mathcal{L}\left\lfloor_{[0,1]}((-\infty, y])\right.&=\mathcal{L}\left\lfloor_{[0,1]}\left(\left\{t: G^{-1}(t) \leq y\right\}\right)\right.\\ &=\mathcal{L}\left\lfloor_{[0,1]}(\{t: G(y) \geq t\})\right.\\ &=G(y) \\ &=\nu((-\infty, y]) \\ &\Rightarrow T^{\dagger}_{\#} \mu =G_{\#}^{-1}\left(F_{\#} \mu\right) \end{aligned}\] -
第二部分证明 \(T^{\dagger}\) 是蒙日形式的最优传输,利用之前的质量不变公式和 \(F_{\#} \mu=\mathcal{L}_{[0,1]}\)
\[\begin{aligned} \inf _{\pi \in \Pi(\mu, \nu)} \mathbb{K}(\pi) &=\int_{0}^{1} d\left(F^{-1}(t)-G^{-1}(t)\right) \mathrm{d} t \\ &=\int_{\mathbb{R}} d\left(x-G^{-1}(F(x))\right) \mathrm{d} \mu(x) \\ &=\int_{\mathbb{R}} d\left(x-T^{\dagger}(x)\right) \mathrm{d} \mu(x) \\ & \geq \inf _{T: T_{\#} \mu=\nu} \mathbb{M}(T) \end{aligned}\]同时 \(\inf _{T: T_{\#} \mu=\nu} \mathbb{M}(T) \geq \min _{\pi \in \Pi(\mu, \nu)} \mathbb{K}(\pi)\) ,因此 \(T^{\dagger}=G^{-1} \circ F\) 是蒙日最优传输
-
Proposition 2.3
定义一个很重要的性质,集合的单调性(这是对于某个测度 \(d\) ),由简单的一个二维情况做例子:
对于 \(\Gamma \subset \mathbb{R}^{2}\),\(\forall \left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right) \in \Gamma\) , \(\Gamma\) 是单调的当:
\[d\left(x_{1}-y_{1}\right)+d\left(x_{2}-y_{2}\right) \leq d\left(x_{1}-y_{2}\right)+d\left(x_{2}-y_{1}\right)\]然后是 Proposition 2.3 的内容:
有 \(\mu, \nu \in \mathcal{P}(\mathbb{R})\),假设在代价函数 \(c(x, y)=d(x-y)\) 意义下的最优传输计划 \(\pi^{\dagger} \in \Pi(\mu, \nu)\),对于任何支撑集中的点 \(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right) \in \operatorname{supp}\left(\pi^{\dagger}\right)\),有
\[d\left(x_{1}-y_{1}\right)+d\left(x_{2}-y_{2}\right) \leq d\left(x_{1}-y_{2}\right)+d\left(x_{2}-y_{1}\right)\]利用反证法证明,若能在支撑集中构造一个 \(\pi^{\dagger}\) 的下界 \(\pi^{*}\) ,且证明 \(\pi^{*} \in \Pi(\mu, \nu)\)
假设在支撑集中存在不单调的点 \(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right) \in \operatorname{supp}\left(\pi^{\dagger}\right)\),那么就有:
\[d\left(x_{1}-y_{1}\right)+d\left(x_{2}-y_{2}\right)-d\left(x_{1}-y_{2}\right)-d\left(x_{2}-y_{1}\right) \geq \eta\]然后在 \((X, \Sigma_X , \mu)\) 和 \((Y, \Sigma_Y , \nu)\) 上分别构造两个闭区间 \(I_{1}, I_{2}, J_{1}, J_{2}\),且满足:
- \[x_{i} \in I_{i}, y_{i} \in J_{i}, i=1,2\]
- \(\forall x \in I_{i}, y \in J_{j}, i, j=1,2,d(x-y) \geq d\left(x_{i}-y_{j}\right)-\varepsilon\) ,且 \(\varepsilon<\frac{\eta}{4}\)
- $I_{i} \times J_{j}$ 不相交;
- $\pi^{\dagger}\left(I_{1} \times J_{1}\right)=\pi^{\dagger}\left(I_{2} \times J_{2}\right)=\delta>0$
这样的闭区间可以通过取的很小构造出,利用这些小区间去构造比 \(\pi^{\dagger}\) 小的测度 \(\tilde{\pi}\),而在小区间之外的部分,则利用原先的最优传输 \(\pi^{\dagger}\) ,因此还需要定义 \(\pi^{\dagger}\) 的投影:
\[\begin{array}{ll} \tilde{\mu}_{1}=P_{\#}^{X} \pi^{\dagger}\left\lfloor I_{1} \times J_{1},\right. & \tilde{\mu}_{2}=P_{\#}^{X} \pi^{\dagger}\left\lfloor I_{2} \times J_{2}\right. \\ \tilde{\nu}_{1}=P_{\#}^{Y} \pi^{\dagger}\left\lfloor_{I_{1} \times J_{1}},\right. & \tilde{\nu}_{2}=P_{\#}^{Y} \pi^{\dagger}\left\lfloor I_{2} \times J_{2}\right. \end{array}\]于是利用最优传输投影 \(\pi^{\dagger}\) 的测度,构造 \(\tilde{\pi}_{12} \in \Pi\left(\tilde{\mu}_{1}, \tilde{\nu}_{2}\right), \tilde{\pi}_{21} \in \Pi\left(\tilde{\mu}_{2}, \tilde{\nu}_{1}\right)\),并定义:
\[\tilde{\pi}(A \times B)=\left\{\begin{array}{ll} \pi^{\dagger}(A \times B) & \text { if }(A \times B) \cap\left(I_{i} \times J_{j}\right)=\emptyset \text { for all } i, j \\ 0 & \text { if } A \times B \subseteq I_{i} \times J_{i} \text { for some } i \\ \pi^{\dagger}(A \times B)+\tilde{\pi}_{12}(A \times B) & \text { if } A \times B \subseteq I_{1} \times J_{2} \\ \pi^{\dagger}(A \times B)+\tilde{\pi}_{21}(A \times B) & \text { if } A \times B \subseteq I_{2} \times J_{1} \end{array}\right.\]\(\tilde{\pi}\) 把小区间的测度挖掉,对于 \((A \times B) \cap\left(I_{i} \times J_{j}\right) \neq \emptyset\) 且 \(A \times B \nsubseteq\left(I_{i} \times J_{j}\right)\) 的情况,利用补集定义:
\[\tilde{\pi}(A \times B)=\tilde{\pi}\left((A \times B) \cap\left(I_{i} \times J_{j}\right)\right)+\tilde{\pi}\left((A \times B) \cap\left(I_{i} \times J_{j}\right)^{c}\right)\]下验证 \(\tilde{\pi} \in \Pi(\mu, \nu)\),取 \(\tilde{\pi}(\mathbb{R} \times B)\) 研究:
-
当 \(B \cap\left(J_{1} \cup J_{2}\right)=\emptyset\)
\[\tilde{\pi}(\mathbb{R} \times B)=\pi^{\dagger}(\mathbb{R} \times B)=\nu(B)\] -
当 \(B \subseteq J_{1}\)
\[\begin{aligned} \tilde{\pi}(\mathbb{R} \times B) &=\tilde{\pi}\left(\left(\mathbb{R} \backslash\left(I_{1} \cup I_{2}\right)\right) \times B\right)+\tilde{\pi}\left(I_{1} \times B\right)+\tilde{\pi}\left(I_{2} \times B\right) \\ &=\pi^{\dagger}\left(\left(\mathbb{R} \backslash\left(I_{1} \cup I_{2}\right)\right) \times B\right)+0+\pi^{\dagger}\left(I_{2} \times B\right)+\tilde{\pi}_{21}\left(I_{2} \times B\right) \\ & \; \Big\Downarrow \; \tilde{\pi}_{21}\left(I_{2} \times B\right)=\tilde{\nu}_{1}(B)=\pi^{\dagger}\left(I_{1} \times\left(B \cap J_{1}\right)\right)=\pi^{\dagger}\left(I_{1} \times B\right) \\ &=\pi^{\dagger}\left(\left(\mathbb{R} \backslash I_{1}\right) \times B\right)+\pi^{\dagger}\left(I_{1} \times B\right) \\ &=\pi^{\dagger}(\mathbb{R} \times B) \\ &=\nu(B) \end{aligned}\]对于 \(B \subseteq J_{2}\) 是一样的,有 \(\tilde{\pi}(\mathbb{R} \times B)=\nu(B)\),同理有 \(\tilde{\pi}(A \times \mathbb{R})=\mu(A)\),推出 \(\tilde{\pi} \in \Pi(\mu, \nu)\)
下证 \(\tilde{\pi}\) 是最优传输:
\[\begin{aligned} & \int_{\mathbb{R} \times \mathbb{R}} d(x-y) \mathrm{d} \pi^{\dagger}(x, y)-\int_{\mathbb{R} \times \mathbb{R}} d(x-y) \mathrm{d} \tilde{\pi}(x, y) \\ &=\int_{I_{1} \times J_{1} \cup I_{2} \times J_{2}} d(x-y) \mathrm{d} \pi^{\dagger}(x, y)-\int_{I_{1} \times J_{2}} d(x-y) \mathrm{d} \tilde{\pi}_{12}(x, y) -\int_{I_{2} \times J_{1}} d(x-y) \mathrm{d} \tilde{\pi}_{21}(x, y) \\ & \geq \delta\left(d\left(x_{1}-y_{1}\right)-\varepsilon\right)+\delta\left(d\left(x_{2}-y_{2}\right)-\varepsilon\right)-\delta\left(d\left(x_{1}-y_{2}\right)+\varepsilon\right)-\delta\left(d\left(x_{2}-y_{1}\right)+\varepsilon\right) \\ &\geq \delta(\eta-4 \varepsilon) \\ &>0 \end{aligned}\]与 \(\pi^{\dagger}\) 是最优传输矛盾,因此知道 \(\operatorname{supp}\left(\pi^{\dagger}\right)\) 在传输代价 \(d\) 的意义下单调
Proof of Theorem 2.1
有传输代价函数 \(d\) 严格凸,连续,由康托洛维奇传输问题最优解的存在性,知存在 \(\pi^{*} \in \prod(\mu, \nu)\) 为最优传输计划,下证 \(\pi^{*}=\pi^{\dagger}\)
- \(\operatorname{supp}\left(\pi^{\dagger}\right)\) 在传输代价 \(d\) 的意义下单调,由传输代价函数 \(d\) 严格凸, \(\operatorname{supp}\left(\pi^{\dagger}\right)\) 就有更强的性质:
这一点利用 \(d\) 严格凸证明,反证法假设 \(y_{1} \leq y_{2}\),设 \(a=x_{1}-y_{1}, b=x_{2}-y_{2},\delta=x_{2}-x_{1}\),由支撑集单调:
\[d(a)+d(b) \leq d(b-\delta)+d(a+\delta)\]设 \(t=\frac{\delta}{b-a} \in \left( 0,1 \right)\) ,则有 \(b-\delta=(1-t) b+t a, a+\delta=t b+(1-t) a\),利用 Jenson 不等式知:
\[d(b-\delta)+d(a+\delta)<(1-t) d(b)+t d(a)+t d(b)+(1-t) d(a)=d(b)+d(a)\]这与单调性矛盾,则支撑集有 \(\forall\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right) \in \Gamma, x_{1}<x_{2} \Rightarrow y_{1} \leq y_{2}\)
-
利用支撑集的性质,可以证明 \(\pi^{*}((-\infty, x],(-\infty, y])=\min \{F(x), G(y)\}\) ,即 \(\pi^{\dagger}=\pi^{*}\):
令 \(A=(-\infty, x] \times(y,+\infty), B=(x,+\infty) \times(-\infty, y]\),由\(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right) \in \Gamma , x_{1} \leq x_{2} \Rightarrow y_{1} \leq y_{2}\),若有 \(\left(x_{0}, y_{0}\right) \in \Gamma\),则
\[\Gamma \subset\left\{(x, y): x \leq x_{0}, y \leq y_{0}\right\} \cup\left\{(x, y): x \geq x_{0}, y \geq y_{0}\right\}\]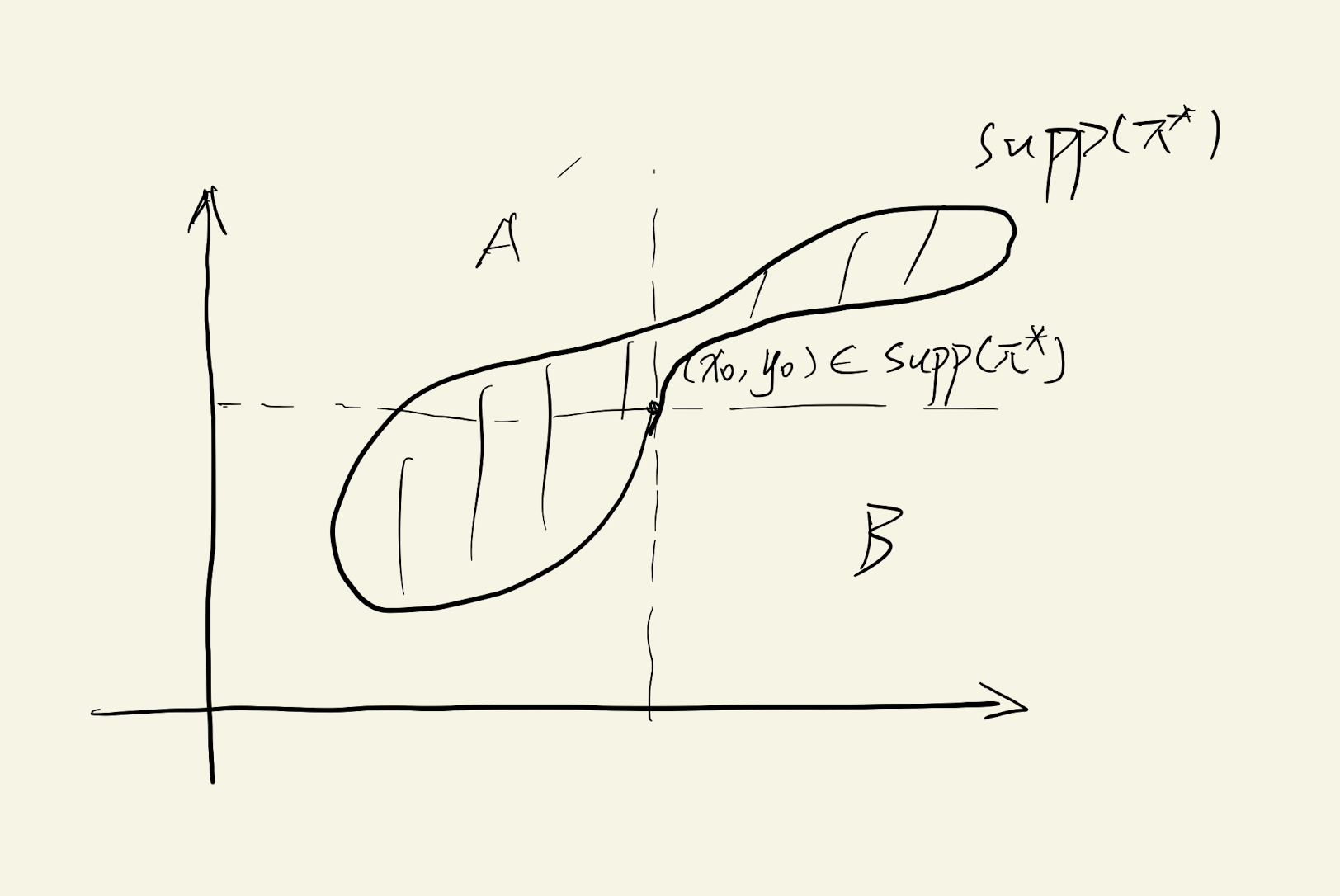
如图所示,由于支撑集的性质,有 \(\pi(A) * \pi(B)=0\),知道 \(\pi^{*}\)测度不大于:
\[\begin{aligned} \pi^{*}((-\infty, x] \times(-\infty, y])=\min \{& \pi^{*}(((-\infty, x] \times(-\infty, y]) \cup A), \left.\pi^{*}(((-\infty, x] \times(-\infty, y]) \cup B)\right\} . \end{aligned}\]进一步的,由于
\[\begin{array}{l} \pi^{*}(((-\infty, x] \times(-\infty, y]) \cup A)=\pi((-\infty, x] \times \mathbb{R})=F(x) \\ \pi^{*}(((-\infty, x] \times(-\infty, y]) \cup B)=\pi(\mathbb{R} \times(-\infty, y])=G(y) \end{array}\]那么 \(\pi^{*}((-\infty, x] \times(-\infty, y])=\min \{F(x), G(y)\}=\pi^{\dagger}((-\infty, x] \times(-\infty, y])\),由此可知 \(\pi^{\dagger}\) 为康托洛维奇最优传输
-
最后证一维最优传输的等价性,\(\int_{\mathbb{R} \times \mathbb{R}} d(x-y) \mathrm{d} \pi^{\dagger}(x, y)=\int_{0}^{1} d\left(F^{-1}(t)-G^{-1}(t)\right) \mathrm{d} t\),也等价于 \(\pi^{\dagger}=\left(F^{-1}, G^{-1}\right)_{\#} \mathcal{L}\lfloor[0,1]\)
进一步的,由于变量变换公式:
\[\int_{\mathbb{R} \times \mathbb{R}} d(x-y) \mathrm{d} \pi^{\dagger}(x, y)=\int_{\mathbb{R} \times \mathbb{R}} d(x-y) \mathrm{d}\left(\left(F^{-1}, G^{-1}\right)_{\#} \mathcal{L}\right)(x, y)=\int_{0}^{1} d\left(F^{-1}(t)-G^{-1}(t)\right) \mathrm{d} t\]Optimal Transport for Discrete Measures
蒙日形式最优传输,在传输代价 \(d\) 形式不定时,存在性很难证明,但是在限定一些特殊情况,比如离散测度下,则可以构造蒙日传输映射集非空的情况,其蒙日形式最优传输一定存在,具体设定如下:
等数量,等密度的两个测度 \(\mu=\frac{1}{n} \sum_{i=1}^{n} \delta_{x_{i}},\nu=\frac{1}{n} \sum_{j=1}^{n} \delta_{y_{j}}\) ,这种情况下蒙日传输映射 \(T: X \rightarrow Y\) 一定存在,比如
\[T\left(x_{i}\right)=y_{\sigma(i)} \quad \sigma:\{1, \ldots, n\} \rightarrow\{1, \ldots, n\}\]对于巴拿赫空间 \(M\) 中一个凸,紧的集合 \(B\) ,定义其极值点集合 \(\mathcal{E}(B)\),代表那些仅有平凡凸组合的点:
\[B \ni \pi=\sum_{i=1}^{m} \alpha_{i} \pi_{i},\pi \in \mathcal{E}(B) \Leftrightarrow \alpha_{i} \in\{0,1\}\]会有两个结论:
Theorem 2.5. Minkowski–Carathéodory Theorem.
\(B \subset \mathbb{R}^{M}\) 是一个非空,凸的,紧集合,\(\forall \pi^{\dagger} \in B ,\exists \; \eta\) ,其支撑集是\(\; \mathcal{E}(B)\) ,对于任意仿射函数 \(f\) :
\[f\left(\pi^{\dagger}\right)=\int f(\pi) \mathrm{d} \eta(\pi)\]或者说,一个凸包 \(B\) 中的点 \(\pi^{\dagger}\),利用凸包的极点集\(\; \mathcal{E}(B)\) 就可以凸表示,且至多用 \(\operatorname{dim}(B)+1\) 即可表示,且基与 \(\pi^{\dagger}\) 无关
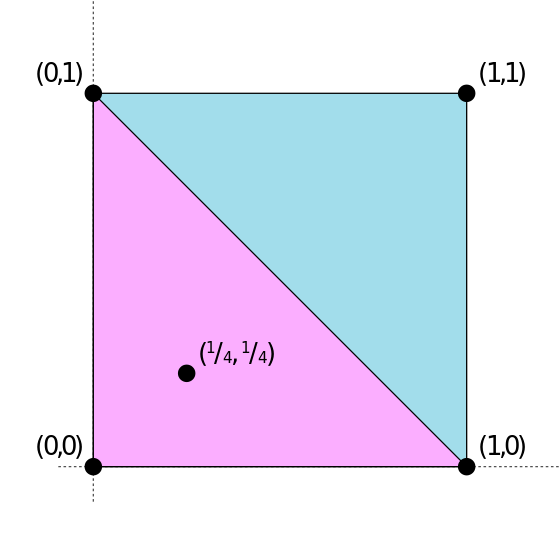
利用数归证明:假设在 \(d-1\) 的情况下都可以如此表示
在 \(d\) 维中,取 \(\pi^{\dagger} \in B,\pi^{\dagger} \notin \mathcal{E}(B)\),在极点集中取 \(\pi^{(0)} \in \mathcal{E}(B)\),做线段 \(\left[\pi^{(0)}, \pi^{\dagger}\right]\) 并延长直到与 \(B\) 的边界相交为点 \(\xi\) ,则线段可以表示,其参数集为\(\left\{\theta:(1-\theta) \pi^{(0)}+\theta \pi^{\dagger} \in B\right\}=[0, \alpha]\),反过来表出 \(\xi=(1-\alpha) \pi^{(0)}+\alpha \pi\),同时有 \(\pi^{\dagger}=\left(1-\theta_{0}\right) \xi+\theta_{0} \pi^{(0)},\theta_{0}=1-\frac{1}{\alpha}\) ,由 \(\xi\) 在边界上,则为 \(d-1\) 的情况,可以基表示:\(\xi=\sum_{i=1}^{n} \theta_{i} \pi^{(i)},\sum_{i=1}^{d} \theta_{i}=1\),因此有
\[\pi^{\dagger}=\sum_{i=1}^{d}\left(1-\theta_{0}\right) \theta_{i} \pi^{(i)}+\theta_{0} \pi^{(0)} \\ \left(1-\theta_{0}\right) \sum_{i=1}^{d} \theta_{i}+\theta_{0}=1\]因此可以 \(\pi^{\dagger}\) 可以凸表示,且 \(\pi^{\dagger}\) 的选择与 \(\pi^{(0)}\) 无关
Theorem 2.6. Birkhoff’s theorem
离散形式的最优传输,等价于一个线性规划,可以利用一个 \(\mathbb{R}^{n \times n}\) 表示,称为 Bistochastic 矩阵,具体来说是:
\[B=\left\{\pi \in \mathbb{R}^{n \times n}: \forall i j, \pi_{i j} \geq 0 ; \forall j, \sum_{i=1}^{n} \pi_{i j}=1 ; \forall i, \sum_{j=1}^{n} \pi_{i j}=1\right\}\]Birkhoff’s theorem指出了这样的矩阵的极点集为置换矩阵:
\[\mathcal{E}(B)=\left\{\pi \in\{0,1\}^{n \times n}: \forall j, \sum_{i=1}^{n} \pi_{i j}=1 ; \forall i, \sum_{j=1}^{n} \pi_{i j}=1\right\}\]-
先证明置换矩阵是极值点:
设矩阵 \(\pi\),定义 \(\pi_{i j}=\delta_{j=\sigma(i)}\) 且 \(\pi \notin \mathcal{E}(B)\),因此存在异于 \(\pi\) 的两点 \(\pi^{(1)}, \pi^{(2)} \in B\),且能表达 \(\pi\) ,为 \(\pi=t \pi^{(1)}+(1-t) \pi^{(2)},t \in(0,1)\),取 \(\pi\) 中为 0 的分量:
\[0=\pi_{i j}=t \pi_{i j}^{(1)}+(1-t) \pi_{i j}^{(2)} \Longrightarrow \quad \pi_{i j}^{(2)}=-\frac{\pi_{i j}^{(1)}}{1-t}<0\]这与之前对于传输矩阵的定义矛盾,则置换矩阵一定是极值点
-
在证明极值点集合 \(\pi \in \mathcal{E}(B)\) 的元素是置换矩阵:
-
先证明极值点中元素形式为 \(\pi_{i j} \in\{0,1\}\):
取一个极点集中元素 \(\pi \in \mathcal{E}(B)\),且不满足 \(\pi_{i j} \in\{0,1\}\),则利用这一点,可以在轮流控制指标 \(i,j\) 的情况下,利用 \(\sum_{i=1}^{n} \pi_{i j_{1}}=1\) 和 \(\sum_{j=1}^{n} \pi_{i_{2} j}=1\) 直到有 \(i_{m}=\imath_{1}\) 时,比如对于 \(\pi_{i_{1} j_{1}} \in(0,1)\),\(\exists \pi_{i_{2} j_{1}} \in(0,1),s.t \; \sum_{i=1}^{n} \pi_{i j_{1}}=1\)
于是有两列序列:
\[\mathcal{I}=\left\{i_{k} j_{k}: k \in\{1, \ldots, m-1\}\right\} \quad \mathcal{I}^{+}=\left\{i_{k+1} j_{k}: k \in\{1, \ldots, m-1\}\right\}\]其有性质:\(i_{k+1} \neq i_{k} \text { and } j_{k+1} \neq j_{k}\),并定义在 \(\pi\) 上定义扰动:
\[\pi_{i j}^{(\delta)}=\left\{\begin{array}{ll} \pi_{i_{k} j_{k}}+\delta & \text { if } i j=i_{k} j_{k} \text { for some } k \\ \pi_{i_{k+1} j_{k}}-\delta & \text { if } i j=i_{k+1} j_{k} \text { for some } k \\ \pi_{i j} & \text { else } \end{array}\right.\]验证 \(\sum_{i=1}^{n} \pi_{i j}^{(\delta)}=\sum_{i=1}^{n} \pi_{i j}+\delta \mid \{i j \in \mathcal{I}: i \in\{1, \ldots, n\}\} \mid -\delta \mid \left\{i j \in \mathcal{I}^{+}: i \in\{1, \ldots, n\}\right\} \mid\)
由于 \(i j \in \mathcal{I} \Leftrightarrow \exists \; i^{\prime} , \; s.t \quad i^{\prime} j \in \mathcal{I}^{+}\) 可知指标集大小一样,则:
\[\sum_{i=1}^{n} \pi_{i j}^{(\delta)}=1,\sum_{j=1}^{n} \pi_{i j}^{(\delta)}=1\]控制扰动 \(\delta=\min \left\{\min \left\{\pi_{i j}, 1-\pi_{i j}\right\}: i j \in \mathcal{I} \cup \mathcal{I}^{+}\right\} \in(0,1)\) ,则可以定义 \(\pi^{(1)}=\pi^{(-\delta)} \neq \pi^{(2)}=\pi^{(\delta)}\),且 \(\pi^{(1)}, \pi^{(2)} \in B\) ,进一步的可以构造出 \(\pi\):
\[\pi=\frac{1}{2} \pi^{(1)}+\frac{1}{2} \pi^{(2)}\]这与极点集的条件矛盾,因此知道极点集中的元素有形式:\(\pi_{i j} \in\{0,1\}\)
-
在证明这样的 \(\pi\) 是一个置换,这根据 \(\forall \; i , \exists \; j^* ,s.t \; \pi_{i j^{*}}=1\) 就可以得知
-
Theorem 2.7 Existence of Optimal Transport Map of Discrete Measurement
对于离散测度的 \(\mu=\frac{1}{n} \sum_{i=1}^{n} \delta_{x_{i}}, \nu=\frac{1}{n} \sum_{j=1}^{n} \delta_{y_{j}}\),存在蒙日形式的最优传输映射
在 \(c_{i j}=c\left(x_{i}, y_{j}\right)\) 意义下,利用 Bistochastic 矩阵,\(B=\left\{\pi \in \mathbb{R}^{n \times n}: \forall i j, \pi_{i j} \geq 0 ; \forall j, \sum_{i=1}^{n} \pi_{i j}=1 ; \forall i, \sum_{j=1}^{n} \pi_{i j}=1\right\}\),康托洛维奇离散形式可以写成:
\[\text { minimise } \frac{1}{n} \sum_{i, j} c_{i j} \pi_{i j} \quad \text { over } \pi \in B\]存在 \(M\) 为康托洛维奇形式的最小,\(\varepsilon>0\) 有并做一个逼近 \(\pi^{\varepsilon} \in B\)
\[M \geq \sum_{i j} c_{i j} \pi^{\varepsilon}-\varepsilon\]令 \(f(\pi)=\sum_{i j} c_{i j} \pi_{i j}\),由 \(B\) 是紧的,凸的,存在一个支撑集为\(\mathcal{E}(B)\) 的测度 \(\eta\) ,由 Minkowski–Carathéodory Theorem 知:
\[f\left(\pi^{\varepsilon}\right)=\int f(\pi) \mathrm{d} \eta(\pi)\]因此,可以放下界:
\[M \geq \int \sum_{i j} c_{i j} \pi_{i j} \mathrm{~d} \eta(\pi)-\varepsilon \geq \inf _{\pi \in \mathcal{E}(B)} \sum_{i j} c_{i j} \pi_{i j}-\varepsilon \geq M-\varepsilon\]取 \(\varepsilon \rightarrow 0\),则 \(\inf _{\pi \in \mathcal{E}(B)} \sum_{i j} c_{i j} \pi_{i j}=M\),由 \(\mathcal{E}(B)\) 紧,则 \(\pi^{\dagger} \in \mathcal{E}(B)\),由 Birkhoff’s theorem 知极值点为置换矩阵,于是康托洛维奇最优传输可以写成一个置换矩阵 \(\sigma^{\dagger}:\{1, \ldots, n\} \rightarrow\{1, \ldots, n\}\) \(\pi_{i j}^{\dagger}=\delta_{j=\sigma^{\dagger}(i)}\),因此可以定义蒙日传输 \(T^{\dagger}: X \rightarrow Y\):
\[T^{\dagger}\left(x_{i}\right)=y_{\sigma}(i)\]当定义一个普通的康托洛维奇传输计划 \(\pi_{i j}=\delta_{y_{j}=T\left(x_{i}\right)}\) 可知:
\[\sum_{i=1}^{n} c\left(x_{i}, T\left(x_{i}\right)\right)=\sum_{i j} c_{i j} \pi_{i j} \geq \sum_{i j} c_{i j} \pi_{i j}^{\dagger}=\sum_{i=1}^{n} c\left(x_{i}, T^{\dagger}\left(x_{i}\right)\right)\]由此蒙日形式等价于康托洛维奇形式,\(T^{\dagger}\) 是蒙日最优传输
Reference
- Matthew Thorpe “Introduction to Optimal Transportation”