符号
| Notation | Meaning |
|---|---|
| \( t \quad\) | time |
| \(y\) | altitude |
| \(v \quad\) | velocity, positive upwards |
| \(F \quad\) | total force, positive upwards |
| \(D \quad\) | aerodynamic drag |
| \(T \quad\) | propulsive thrust |
| \(\Delta t \quad\) | time step |
| \(\rho\) | air density |
| \(g\) | gravitational acceleration |
| \(m\) | mass |
| \(C_{D}\quad\) | drag coefficient |
| \(A \quad\) | drag reference area |
| \(\dot{m}_{\text {fuel }}\) | fuel mass flow rate |
| \(u_{e} \quad\) | exhaust velocity |
| \(i\) | time index |
火箭模型
自己去运算,甚至搭建一个火箭模型,是一件很有意思的事情。无论是SpaceX还是最近的天问一号,无一不是
无论是哪一种火箭,其受力基本上都是三种,火箭发动机产生的推力,火箭在大气中收到的阻力,以及火箭附近的星体对其的引力:

-
推力
推力一般通过发动机产生燃烧燃料后,向运动方向后方喷出,由喷出气体的动量产生的推力和发动机腔体内部压力和大气压力两部分组成:
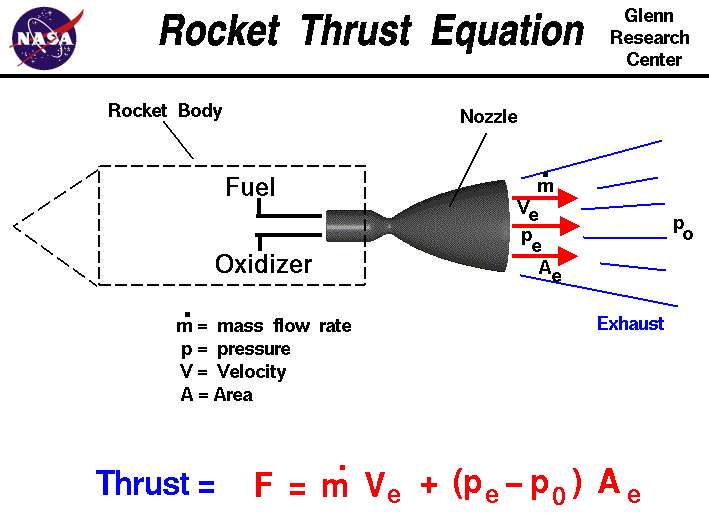
由上式可知,火箭的推力主要来自于两部分,第一部分是高速喷出的气体,这部分由牛顿第三定律的推导,转化成了推力,值得一提的是,为了增加喷出的质量(气体流)的速度,设计师往往在火箭的腔体上做特别的设计,以加强火箭的气体喷出速度,另外火箭发动机腔体内部的高压和外部较为稀薄的气压,产生的气压差,这一部分也会增加一部分推力,但是推力的主体是第一部分产生的力
-
重力
重力本质上是行星对于火箭的引力,因此高推力火箭需要计算高度对于重力的影响,而在火箭入轨后,引力充当了向心力的作用,也因此,放射的火箭有三种情况,采用牛顿大炮的叙事:
- 入轨时未达到第一宇宙速度:
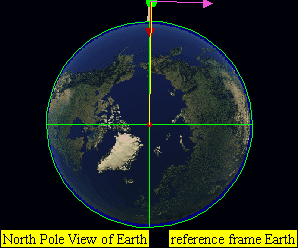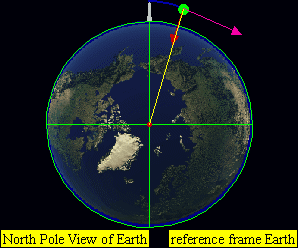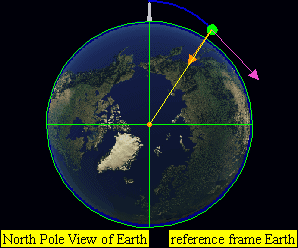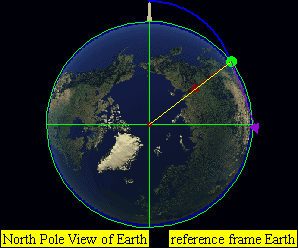
-
入轨时达到第一宇宙速度但是未能超过第二宇宙速度(逃逸速度):
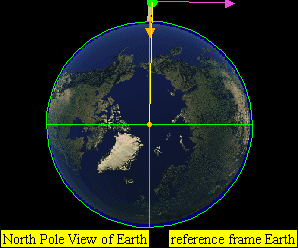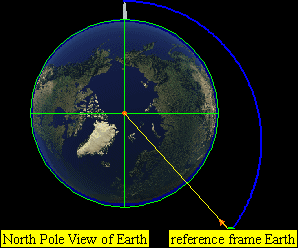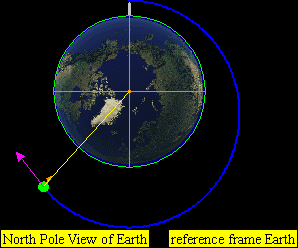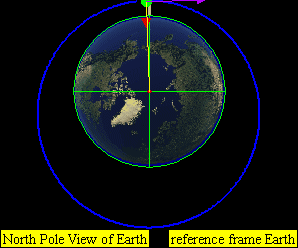
-
如果速度非常快,火箭将会沿着一个抛物线(当速度恰好为第二宇宙速度)或者双曲线(当速度大于第二宇宙速度)轨道逃离地球。
于是,考虑轨道火箭的发射,在足够的海拔高度处,大气非常的稀薄以至于可以无视,同时火箭的发动机熄火没有推力的情况下,火箭是只受一个引力的,于是轨道火箭的发射,就变成了在计算好的合适的高度,使得火箭以一个合适的速度进入轨道:
\[G \frac{M m}{R^{2}}=m \frac{v_{1}^{2}}{R} \\ v_{1}=\sqrt{\frac{G M}{R}}\]
- 入轨时未达到第一宇宙速度:
-
空气动力学力
最后一部分是空气动力学的力,往往有两个力,一个是阻力,一个是升力,值得一提的两点
-
飞行器一般都需要考虑两种空气动力学力,升力与阻力,与飞机相反,火箭的阻力/升力非常大,升力往往起到稳定飞行姿态的作用,这点在具体程序设计中会有类似的实现
-
关键的是,比起阻力参数,可以直观的通过几何形状,和经验估算,飞行器的升力参数,是要通过风洞实验得知,在网上非常难以查到
综上两点,空气动力学力,建模时只考虑作用较大的阻力
\[D=\operatorname{C_d} \frac{\rho V^{2} }{2} A\]其中 \(\rho\) 的值由下表提供:

查阅SpaceX的资料可以知道Falcon火箭的 \(C_d\) 和几何参数进而推算 \(A\)
-
模型火箭模型
-
模型火箭的历史
严格的来说,火箭的原型很早就有了,可以追溯到中国的南宋时期,其制造的黑火药推进剂的飞行物,被投入战争中使用,宋朝时的火箭没有正经的发射架,是通过弩来发射的,其构造有一个带孔的管子,里面填充了黑火药和一个棍子来帮助火箭姿态稳定,然后在接下来的几百年间,逐步改进。
而在西方,比利时的工程师在1591年的时候,提出了多级火箭的构想,每一个火箭在前一级燃烧完成后,被点燃,后一级火箭被丢弃,这和现代的多级火箭已经相差不远了。
现代意义上的模型火箭,主要是由美国主导建立的体系:
-
第一架现代模型火箭:由 Orville Carlisle 与他的弟弟 Bobert 设计,本意是想去做一个由火箭推力的飞行器的他们,在偶然读了文章后,发现由于流行文化的影响,许多年轻人正在尝试制作自己的模型火箭,然后他们花了三年的时间,设计,完成了原型机,最后顺利的拿到了安全证书
-
第一家模型火箭公司是 Model Missiles Incorporated (MMI),位于科罗拉多丹佛,而比较重要的公司 Estes Industries 是由 Estes 在1958年建立的,该公司占据了美国市场的大部分,创始人是一个烟花匠家的孩子, 该公司早期,其实是 MMI 的供货商,后来在 MMI 经营不善后,独立出去
-
-
模型火箭的结构
下面是模型火箭根据推力进行的分级(Estes标准)。火箭燃料最高等级为O,但是G级以上的就被分类成为高推力火箭
Class Total Impulse (Metric Standard) 1/4A 0.313-0.625 N·s 1/2A 0.626-1.25 N·s A 1.26-2.50 N·s B 2.51-5.0 N·s C 5.01-10 N·s D 10.01-20 N·s E 20.01-40 N·s F 40.01-80 N·s G 80.01-160 N·s 物理上最大的黑火药模型火箭发动机一般到E级,因为黑火药块比较脆。如果大型黑火药发动机是火箭的更高推力的发动机,比如说超过了建议的最大起飞重量,又或者有过多的加热/冷却循环(例如,在高温的密闭发动机中),则推进剂装药可能会出现细碎的裂痕。这些裂痕增加了推进剂接触空气表面积,因此当发动机点火时,推进剂燃烧得更快,并产生比发动机内部正常的内腔压力更大的压力。该压力可能会超过发动机外壳的强度(一般是纸板),并导致电机爆裂。爆裂的电动机可能会对模型火箭造成损害,范围从简单的电动机管或车身管破裂到回收系统的猛烈弹射(偶尔会着火)
下图为模型火箭的发动机结构:
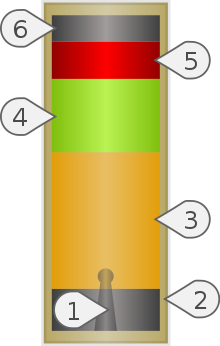
因此,额定功率高于D到E的火箭发动机通常使用由高氯酸铵,铝粉和硬质塑料外壳中包含的橡胶状粘合剂物质制成的复合推进剂。这种推进剂类似于航天飞机的固体火箭助推器中使用的推进剂,不像黑火药那么脆弱,从而提高了发动机的可靠性和推进剂的稳定性。这些电动机的等级大小从D到O不等。复合电动机每单位重量产生的脉冲(特定脉冲)比黑粉电动机更大。 还提供可再装的复合推进剂电动机。这些是商业生产的电动机,需要用户将推进剂颗粒,O形圈和垫圈(以容纳膨胀气体)组装,延迟颗粒和喷射电荷到特殊的不易碎的铝制电动机机壳中,该机壳具有旋入式或卡入式端部(封闭)。可重装电动机的优点是成本:首先,由于主壳体是可重用的,因此重装成本明显低于相同脉冲的一次性电动机。其次,大型复合发动机的组装劳动强度大且难以自动化。将这项任务分担给消费者可以节省成本。可重装电动机从D级到O级都有。 电动机用电火柴进行电点火,火柴包括短长度的热原涂层镍铬合金,铜或铝桥线,将其推入喷嘴,并用防火棉,橡皮筋,塑料塞子或胶带将其固定在适当的位置。推进剂的顶部是跟踪延迟装药,该装药会产生烟雾,但实际上不会产生推力,这是因为火箭减速并飞弧。延迟电荷耗尽后,它会点燃喷射电荷,用于部署恢复系统。
-
模型火箭的物理模型
最简单的系统,就是不考虑地心地固坐标系的情况下,讲地面考虑成平地,同时忽略质量的瞬时变动,继续使用牛顿第二系统去建立模型,只能适用于小型模型火箭,往往不会进入地球轨道,同时其极限高度也比较小,往往被限制在对流层内,因此阻力中的大气情况比较好估算,直接采用地表的大气压即可
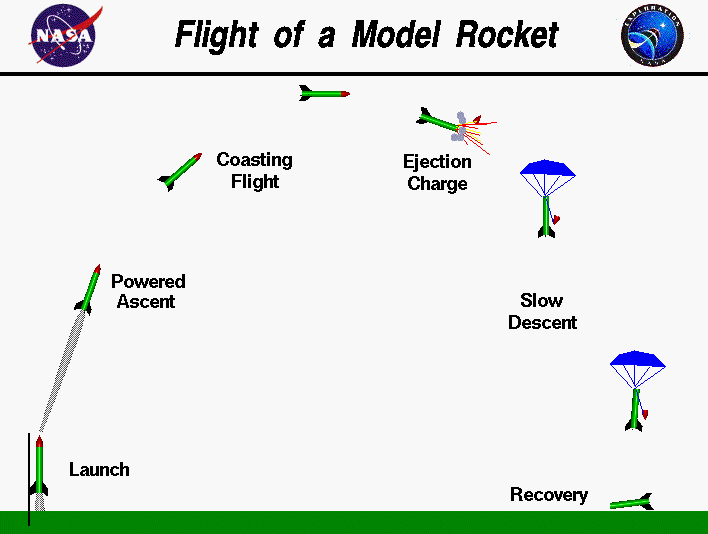
现在做的火箭模型不考虑回收的环节
因此是一个有一定发射的初始角度,可能有一个初速度,在运动过程中受推力,重力和空气动力学力三个力影响
建立其动力模型:
\[\begin{array}{l} \left\{\begin{array}{l} y^{\prime}=v \cos (\theta) \\ x^{\prime}=v \sin (\theta) \\ m \vec{v}^{\prime}=\vec{T}-\vec{D}-\vec{G} \\ m v_{y}^{\prime}=(T-D)\cos(\theta)-G\\ m v_{x}^{\prime}=(T-D)\sin(\theta) \\ D=\frac{1}{2}\rho c_D A v^2 \\ m^{\prime}=-{m}_{f u e l}^{\prime} \\ T = m^{\prime}_{f u e l} u_{e} \\ m^{\prime}_{f u e l} = c \\ G = mg\frac{R_e^2}{(y+R_e)^2} \end{array}\right. \\ \end{array}\]整理后得出:
\[\left\{\begin{array}{l} y^{\prime}=v_{\|} \cos (\theta) \\ x^{\prime}=v_{\|} \sin (\theta) \\ v_{\|}^{\prime}=\left(-\frac{m^{\prime}}{m} u_{e}-\frac{\rho c_{D} A}{m} v^{2}\right)-g \frac{R_{s}^{2}}{\left(y+R_{e}\right)^{2}} \cos (\theta) \\ \theta^{\prime}=g \frac{\sin (\theta)}{v_{\|}} \\ m^{\prime}=-c \end{array}\right.\]到达最高点当:\(\frac{d \theta}{d t}=0\),然后开始下落
-
模型火箭的数值计算
-
数值计算模型
当考虑阻力时,就无法显式的计算出模型火箭的发射轨迹了,因此需要数值计算
考虑离散化的模型: \(\begin{aligned} t & \rightarrow t_{i} \\ h(t) & \rightarrow h_{i} \\ V(t) & \rightarrow V_{i} \end{aligned}\)
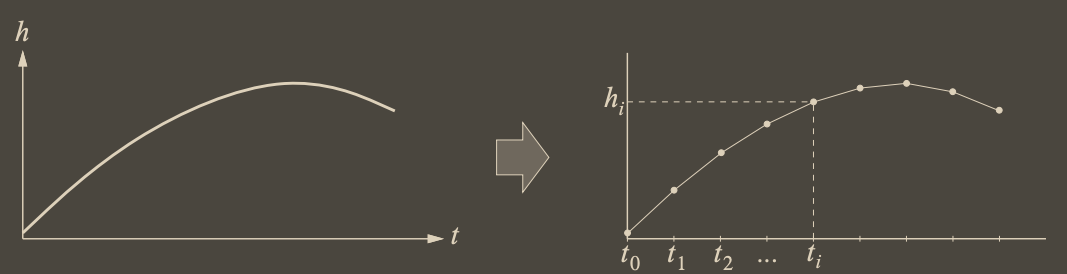
而运动方程可以做离散化处理成:
\[\dot{y}_{i}=\frac{d y}{d t} \simeq \frac{\Delta y}{\Delta t}=\frac{y_{i+1}-y_{i}}{t_{i+1}-t_{i}} \\ \dot{x}_{i}=\frac{d x}{d t} \simeq \frac{\Delta x}{\Delta t}=\frac{x_{i+1}-x_{i}}{t_{i+1}-t_{i}} \\ \dot{V}_{i}=\frac{d V}{d t} \simeq \frac{\Delta V}{\Delta t}=\frac{V_{i+1}-V_{i}}{t_{i+1}-t_{i}} \\ \dot{m}_{i}=\frac{d m}{d t} \simeq \frac{\Delta m}{\Delta t}=\frac{m_{i+1}-m_{i}}{t_{i+1}-t_{i}}\]然后就可以得出根据时间 \(t\) 插值:
\[\begin{aligned} y_{i+1} &=y_{i}+\left(V_{i}\right)\sin(\theta)\left(t_{i+1}-t_{i}\right) \\ x_{i+1} &=x_{i}+\left(V_{i}\right)\cos(\theta)\left(t_{i+1}-t_{i}\right) \\ \theta_{i} &= \arctan(\frac{y_{i+1}-y_i}{x_{i+1}-x_i})\\ V_{i+1} &=V_{i}+\left(-g-\frac{1}{2} \rho V_{i}\left|V_{i}\right| \frac{C_{D} A}{m_{i}}+\frac{V_{i}}{\left|V_{i}\right|} \frac{\dot{m}_{\text {fuel }} u_{e_{i}}}{m_{i}}\right)\left(t_{i+1}-t_{i}\right) \\ m_{i+1} &=m_{i}+\left(-\dot{m}_{\text {fuel }_{i}}\right)\left(t_{i+1}-t_{i}\right) \end{aligned}\]
-
-
模型结果
火箭的物理参数设定:
\[\begin{array}{l} \left\{\begin{array}{l} h_{0} &=0 \mathrm{m}\\ m_{0} &=0.15 \mathrm{kg} \\ m_{\text {fuel }} &=0.03 \mathrm{kg} \\ u_{e} &=550 \mathrm{m} / \mathrm{s} \\ A &=0.001 \mathrm{m}^{2} \\ \rho &=1.22 \mathrm{kg} / \mathrm{m}^{3} \\ C_{D} &=0.35 \end{array}\right. \\ \end{array}\]然后就是不同的发射的参数设定:
-
首先是
\[\begin{array}{l} \left\{\begin{array}{l} m_{\text {fuel }} &= 0 \\ theta &= 6(D)\\ V_{0} &=100 \mathrm{m} / \mathrm{s} \\ \end{array}\right. \\ \end{array}\]这样的模型设定,就是炮弹飞行的轨迹:
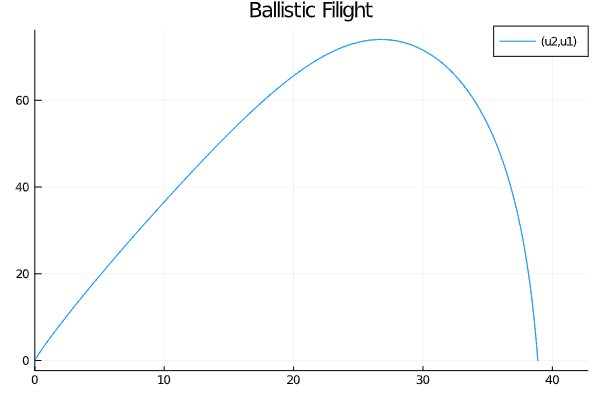
而其飞行速度变化的状态为:
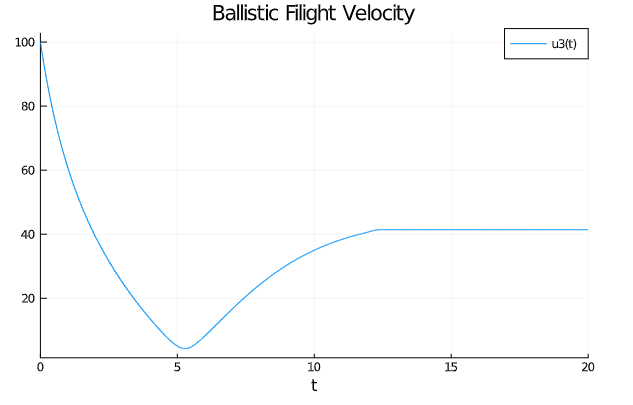
-
然后是比较小推力的火箭,推力的调节是依靠燃料喷射速度的,这和发动机的设计有关
\[\begin{array}{l} \left\{\begin{array}{l} m_{\text {fuel }} &= 0.05 \\ theta &= 6(D)\\ V_{0} &=0.1 \mathrm{m} / \mathrm{s} \\ \end{array}\right. \\ \end{array}\]这样的模型设定,就是比较低推力模型火箭飞行的轨迹:
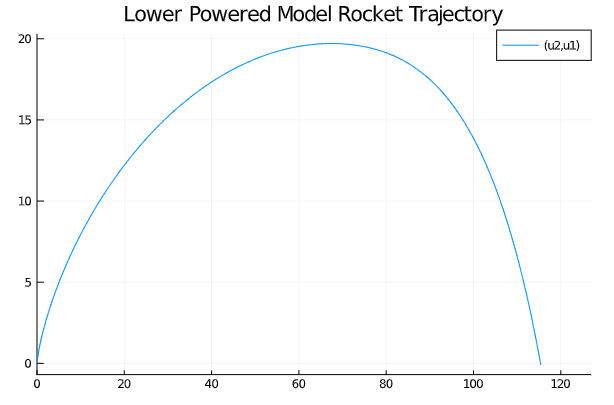
而其飞行速度变化的状态为:
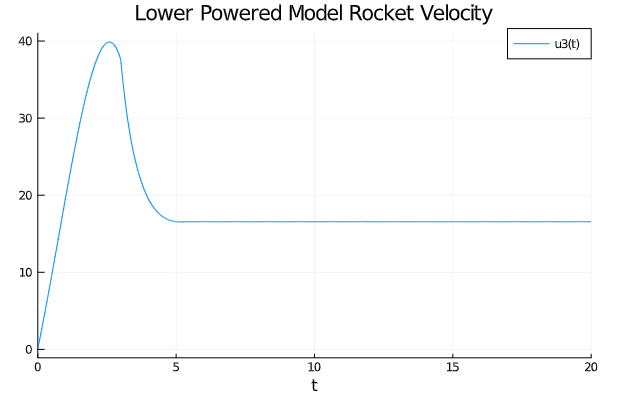
-
最后是高推力火箭
\[\begin{array}{l} \left\{\begin{array}{l} m_{\text {fuel }} &= 0.36 \\ theta &= 6(D)\\ V_{0} &=0.1 \mathrm{m} / \mathrm{s} \\ \end{array}\right. \\ \end{array}\]这样的模型设定,就是比较高推力模型火箭飞行的轨迹:
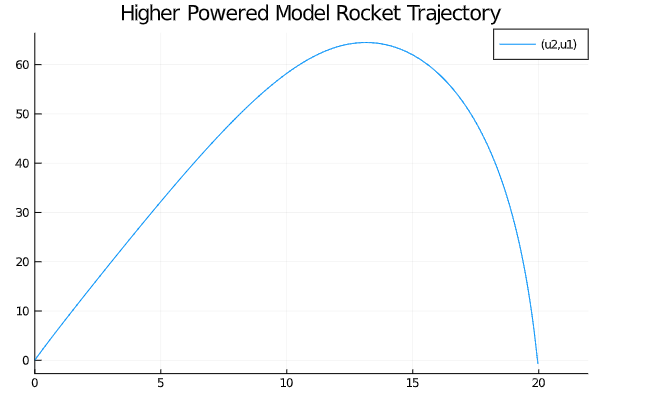
而其飞行速度变化的状态为:
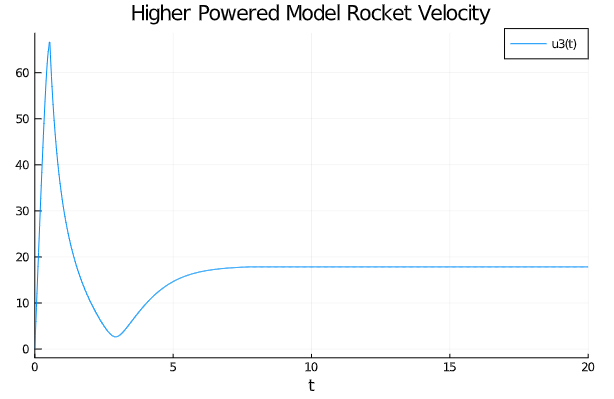
轨道火箭模型
-
轨道火箭的历史
在轨道火箭不到半个多世纪的历史中,人类已经多次发射了轨道火箭:
Name Debut Launches Vostok 1961 6 Mercury 1962 4 Voskhod 1964 2 Gemini 1965 10 Soyuz 1967 142 Apollo 1968 15 Shuttle 1981 134 Shenzhou 2003 7 Dragon 2 2020 1 Total - 321 轨道火箭其实很早就有了构想,主要由苏格兰天文学家和 William Leitch 在1861年的论文《穿越太空之旅》中发表了有关使用火箭进行太空旅行的第一个理论建议。Tsiolkovsky 的作品更广为人知(尽管在俄罗斯以外并不广为人知),该书发表于1903年,“通过反应装置对宇宙空间的探索”。Tsiolkovsky 一生中的火箭工作没有得到充分的赞赏。
但是他影响了Sergey Korolev,他成为斯大林领导下的苏联的首席火箭设计师,开发了洲际弹道导弹,携带核武器作为对付美国轰炸机的对策。 1957年10月4日,使用 R-7 Semyorka导弹发射了世界上第一颗人造地球卫星Sputnik 1,并于1961年4月12日在沃斯托克1号发射了第一颗绕地球轨道的载人飞船,航天员就是著名的加加林。
Robert H. Goddard在1919年发表的论文《A Method of Reaching Altitudes》中,太空飞行成为一种工程可能性。他将de Laval喷嘴应用于液体燃料火箭的效率提高到足以使行星际旅行成为可能。他还在实验室证明火箭可以在太空真空中工作 (!!!但是,他的工作并未受到公众的重视)。 1918年11月11日与德国的停战协定击败了他在第一次世界大战中获得陆军用火箭推进武器合同的尝试。在私人财政支持下,他是1926年第一个发射液体燃料火箭的人。戈达德的论文在他的领域在国际上极具影响力。
在第二次世界大战期间,V-2火箭被研制,并被纳粹德国用作武器。V-2火箭不仅打到了伦敦,同时在1944年6月的一次试飞中,一枚这样的火箭以189公里的高度到达太空,成为人类历史上第一个进入太空的物体。第二次世界大战结束时,Wernher von Braun 在内的大部分V-2的相关科学家都投降了美国,并被派遣到美国的弹道导弹工作,成为了美国陆军弹道导弹局。
诸如朱诺一号和阿特拉斯等导弹的这项工作使1958年2月1日发射了第一颗美国卫星Explorer 1,并于1962年2月20日发射了美国第一个在轨道上的 John Glenn ,在第7友谊中。中心的 Von Braun 监督了一种更大的火箭,称为“土星”的研制,该火箭,即阿波罗11号,使美国能够于1969年7月,将两个宇航员尼尔·阿姆斯特朗和巴斯·奥尔德林送上月球并返回。
-
轨道火箭的结构
模型火箭的设计,当然就比较简单了可以像装满黑色粉末的纸板管一样简单,但是要制造出高效,准确的火箭或导弹,则需要克服许多难题。主要困难包括冷却燃烧室,泵送燃料(在液体燃料的情况下)以及控制和校正运动方向。
-
组件
火箭由推进剂,放置推进剂的地方(例如推进剂箱)和喷嘴组成。它们可能还具有一个或多个火箭发动机,方向稳定装置(例如鳍片,游标发动机或用于推力矢量的发动机万向架,陀螺仪)以及将这些组件固定在一起的结构(通常为单壳)。旨在用于高速大气的火箭弹还具有空气动力学整流罩,例如前锥体,通常可容纳有效载荷。
除了这些组件之外,火箭还可以具有许多其他组件,例如尾翼,着陆用的降落伞,甚至在某种意义上还可以是人(载人火箭),往往火箭会安装有制导系统。
-
火箭发动机

火箭发动机采用喷射推进原理。为火箭提供动力的火箭发动机种类繁多。当前大多数火箭是化学动力火箭(通常是内燃机,但有些采用可分解的单推进剂),可喷射热流。火箭发动机可以使用气体推进剂,固体推进剂,液体推进剂或固体和液体的混合混合物。一些火箭使用的热量或压力来自推进剂的化学反应以外的来源,例如蒸汽火箭,太阳能火箭,核热火箭发动机或简单的加压火箭,例如水火箭或冷气推进器。对于可燃推进剂,在燃烧室内的燃料和氧化剂之间会引发化学反应,并且所产生的热气体会从火箭向后的一端从一个或多个火箭发动机喷嘴中加速出来。这些气体通过发动机的加速在燃烧室和喷嘴上施加力(“推力”),从而推动车辆行驶(根据牛顿第三定律)。这实际上是由于喷嘴孔使燃烧室壁上的力(压力乘以面积)不平衡所致。在其他任何方向都没有这种情况。喷嘴的形状还通过沿着火箭的轴线引导废气而产生力。
-
推进剂
火箭推进剂是通常以某种形式的推进剂罐或外壳形式存储的物质,然后用作以流体射流形式从火箭发动机喷出以产生推力的推进性物质。对于化学火箭,推进剂通常是燃料,例如液态氢或煤油,并与氧化剂(例如液态氧或硝酸)一起燃烧,产生大量非常热的气体。氧化剂与推进剂在燃烧室中混合,或者固体燃料中预混合。有时,推进剂不会燃烧,但仍会发生化学反应,并且可以是可催化分解为热气的“单推进剂”,例如肼,一氧化二氮或过氧化氢。
或者,可以使用可以在外部加热的惰性推进剂,例如蒸汽火箭,太阳热火箭或核热火箭。对于较小的,性能较低的火箭(例如姿态控制推进器),它们不需要较高的性能,可以将加压流体用作推进剂,使其仅通过推进喷嘴逸出航天器。
-
轨道火箭的发射阶段
-
发射
火箭是目前能够到达轨道或超越轨道的唯一手段。其他非火箭航天发射技术尚未建立,或仍缺乏轨道速度。航天飞机的火箭发射通常从一个太空港(宇宙飞船)开始,宇宙飞船可能配备了用于垂直火箭发射的发射装置和发射台,以及用于运载火箭和机翼航天飞机起降的跑道。出于噪声和安全原因,太空港的位置远离人类居住。洲际弹道导弹有各种特殊的发射设施。
发射通常仅限于某些发射窗口。这些窗口取决于天体和轨道相对于发射场的位置。影响最大的往往是地球本身的自转。一旦发射,轨道通常位于相对恒定的平面内,与地球轴成固定角度,并且地球在该轨道内旋转。
发射台是固定的结构,旨在派遣机载车辆。它通常由发射塔和火焰沟组成。它被用于架设,加油和维护运载火箭的设备所包围。在发射之前,火箭可能重达数百吨。 STS-1上的哥伦比亚号航天飞机起飞时重2030吨(4480000磅)。
-
进入太空
最常用的外层空间定义是指距离地球表面100公里(62英里)的卡尔曼线以外的所有事物。美国有时将外层空间定义为海拔超过50英里(80公里)的所有事物。
火箭发动机是目前进入太空的唯一实用手段。由于缺少氧气,传统的飞机发动机无法到达太空。火箭发动机将推进剂排出以提供向前的推力,从而产生足够的速度变化以到达轨道。
对于载人发射系统,经常安装发射逃生系统,以使宇航员在紧急情况下能够逃生。
-
离开轨道
对月球和行星际航行而言,实现封闭的轨道不是必须的。俄国早期的航天器没有进入轨道就成功地达到了很高的高度。美国宇航局曾经考虑将阿波罗飞行任务直接发射到月球轨道上,但采取了先进入临时停车轨道然后在几条轨道上分别燃烧然后再飞向月球轨道的策略。这会增加推进剂的成本,因为停放轨道的近地点必须足够高以防止再次进入,而直接注入的近地点会任意低,因为它将永远无法到达。
但是,停车轨道方法在几个重要方面大大简化了阿波罗任务计划。它大大拓宽了允许的发射窗口,增加了成功发射的机会,尽管在倒计时期间存在一些技术问题。停车轨道是一个稳定的“任务平台”,在发射后,乘员和控制人员有几个小时可以彻底检查航天器,然后再进行长时间的登月飞行。如有必要,机组人员可以迅速返回地球,或者可以进行另一次地球轨道飞行任务。停车轨道还提供了跨月轨迹,避免了范艾伦辐射带最密集的部分。
阿波罗飞行任务通过尽可能降低其高度来最大程度地降低停车轨道的性能损失。例如,阿波罗15号使用了92.5 nmi x 91.5 nmi(171 km x 169 km)的异常低的停车轨道(甚至对于Apollo),那里的大气阻力很大。但是通过从土星五号的第三阶段持续排出氢气可以部分克服它,并且在任何情况下都可以短暂停留。
机器人任务不需要中止能力或将辐射最小化,并且由于现代发射器通常会遇到“瞬时”发射窗口,因此对月球和其他行星的太空探测器通常使用直接注入来最大化性能。尽管有些人可能会在发射序列中短暂滑行,但在烧伤将它们注入地球逃逸轨迹之前,它们并没有完成一个或多个完整的停车轨道。
请注意,天体的逃逸速度会随着其上方的高度而降低。但是,对于船舶来说,尽可能在接近地面的地方燃烧燃料是更省油的,这是解释与建立停车轨道安全近地点有关的性能损失的另一种方式。
未来的载人航天飞行任务计划通常包括在地球轨道上进行最后的车辆组装,例如NASA的Orion航天器和俄罗斯的Kliper / Parom串联。
-
-
轨道火箭的物理模型
-
模型建立
如果要考虑到轨道火箭甚至向火星发射的火箭,由于其入轨后在地表的投影,距离发射基地已经有相当的距离,不能把地球处理成平地,而需要以地心为中心,建立地心地固坐标系(这部分以NASA在1998年发射的火星气象卫星作为图例)
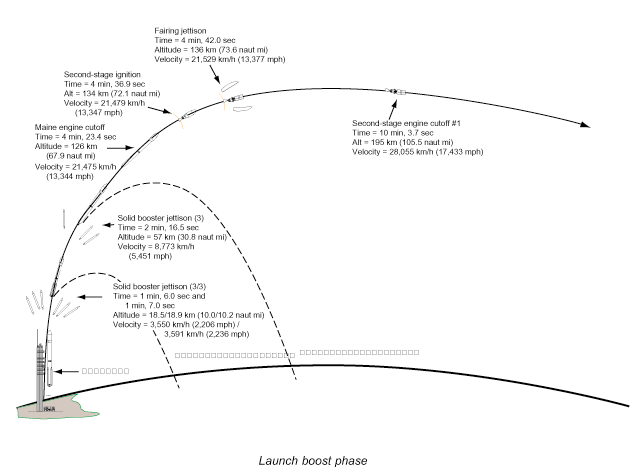
气象火箭在SECO-1阶段大致进入轨道,而在地图上的体现如下图,为状态1到状态2:
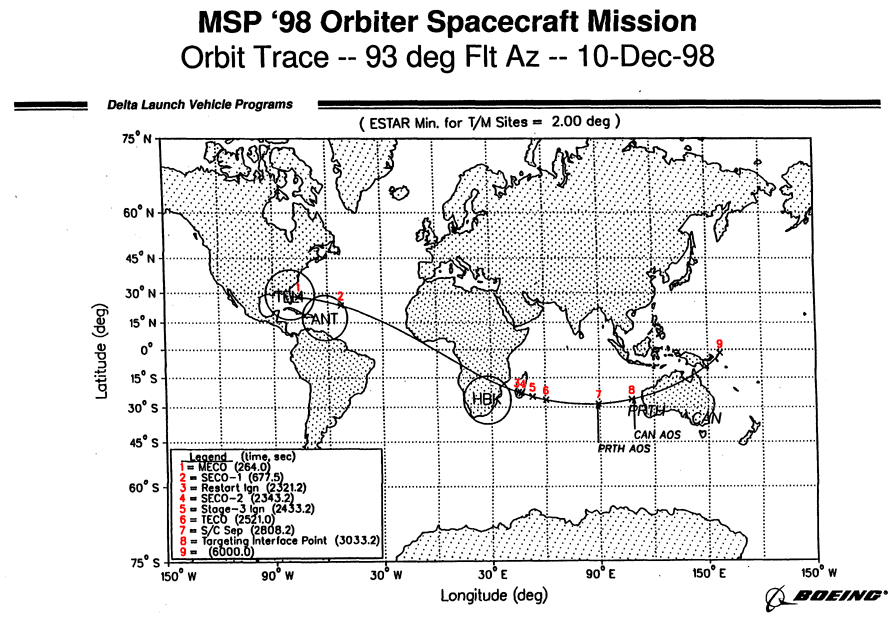
为此可视化的得出,需要采用如地心地固坐标系这样的处理:
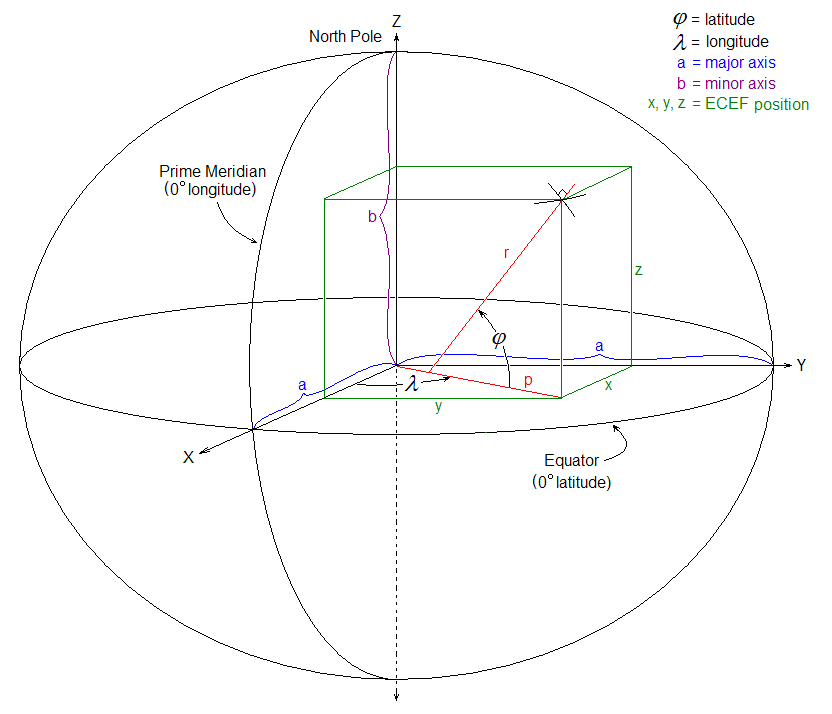
为了方便处理,暂时不考虑地球各点微弱的重力差异,就将地球处理成一个完美球形,地表 \(g\) 值就取 \(9.80665m/s\)
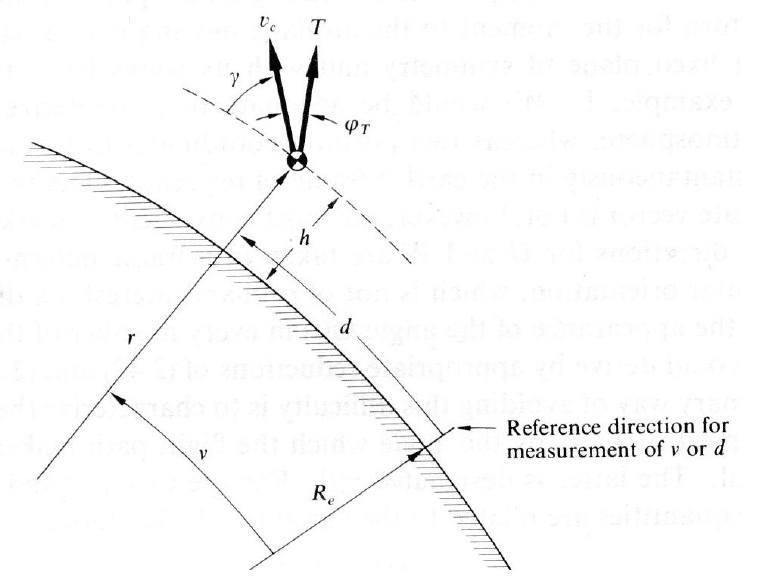
考虑火箭的速度与轨道平行,这样有两个好处:
- 火箭此时不用考虑升力影响
- 火箭
建立其对应的模型:
\[\begin{array}{l} \left\{\begin{array}{l} \tan \theta=\frac{R d \rho}{d R}\Rightarrow R \frac{\varphi^{\prime}}{R^{\prime}}=\frac{\varphi^{\prime}}{\ln R^{\prime}} \\ d v=\frac{R d\varphi}{\sin \theta} \Rightarrow v^{\prime} \sin \theta=R \varphi^{\prime} \\ v ^{\prime}\cos \theta=R^{\prime} \\ m \nu^{\prime}=F=T-D-G \\ D=\rho c_D A v^2 \\ m=-\dot{m}_{f u e l} \\ T=\dot{m}_{f u e l} u_{e} \\ G = mg\frac{R_e^2}{R^2} \\ \end{array}\right. \\ \end{array}\]当考虑到轨道火箭喷出的气体速度较大的时候,牛顿第二定理不再适用,应当考虑动量定理,因此修正方程:
\[\begin{array}{l} \left\{\begin{array}{l} \tan \theta=\frac{R d \rho}{d R}\Rightarrow R \frac{\varphi^{\prime}}{R^{\prime}}=\frac{\varphi^{\prime}}{\ln R^{\prime}} \\ d v=\frac{R d\varphi}{\sin \theta} \Rightarrow v^{\prime} \sin \theta=R \varphi^{\prime} \\ v^{\prime}\cos \theta=R^{\prime} \\ \begin{array}{l} m d v-d m_{f u e l}=(T-D-G) d t \Rightarrow m v^{\prime}-m^{\prime} u_{e}=T-D-G \end{array} \\ D=\rho c_D A v^2 \\ m=-\dot{m}_{f u e l} \\ T=\dot{m}_{f u e l} u_{e} \\ G = mg\frac{R_e^2}{R^2} \end{array}\right. \\ \end{array}\] -
数值计算结果
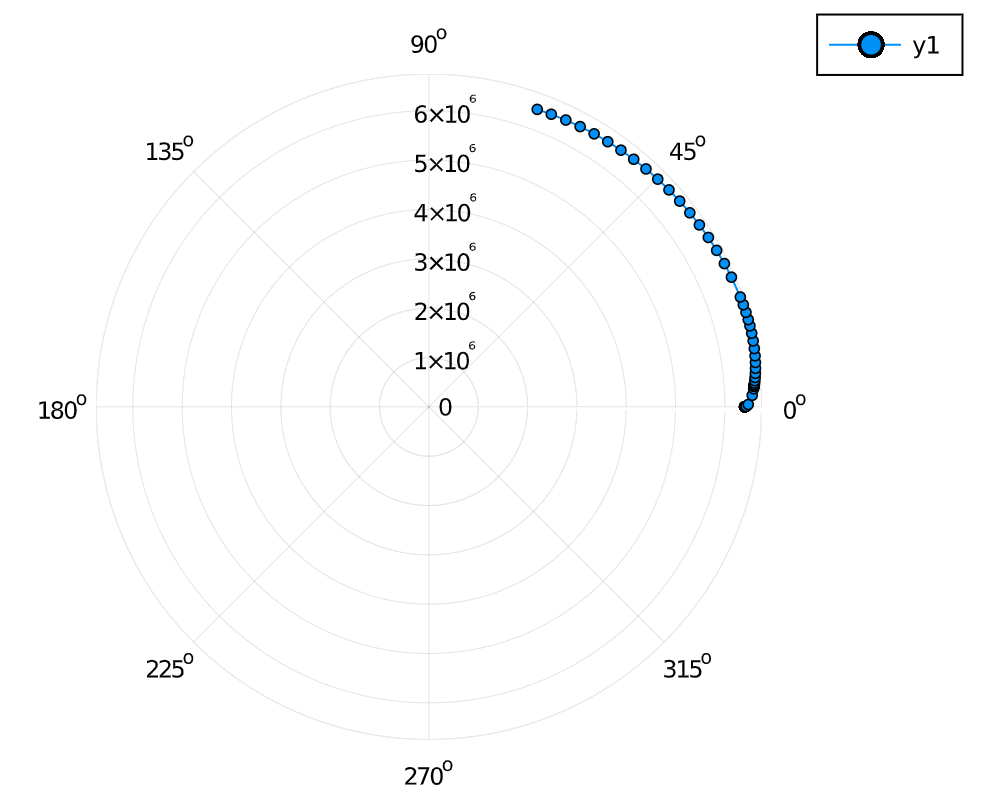
计算的情况是两种,一种是进入轨道的设定
parameter value \(m_{rocket}\) 33800.0 \(m_{fuel1}\) 367500.0 \(m_{fuel2}\) 140000.0 \(t_{inject_1}\) 330.0 \(t_{inject_2}\) 810.0 \(v_{limit1}\) 100.0 \(v_{limit2}\) 400.0 \(v_{limit3}\) 6000.0 \(p_{e}\) 9.7\(\times\)1000000 \(massflow\) 273.6 \(Area_{chamber}\) pi \(\times\) 0.92^2 \(u_e\) 3413 \(T1\) 6806000 \(T2\) 934000 \(R0\) 6400000.0 \(k_{aero}\) 3.7^2 \(\times\)0.25\(\times\) 1/2 \(v_0\) 10.0 \(theta0\) 6 其发射以后,会进入一个封闭的轨道为:
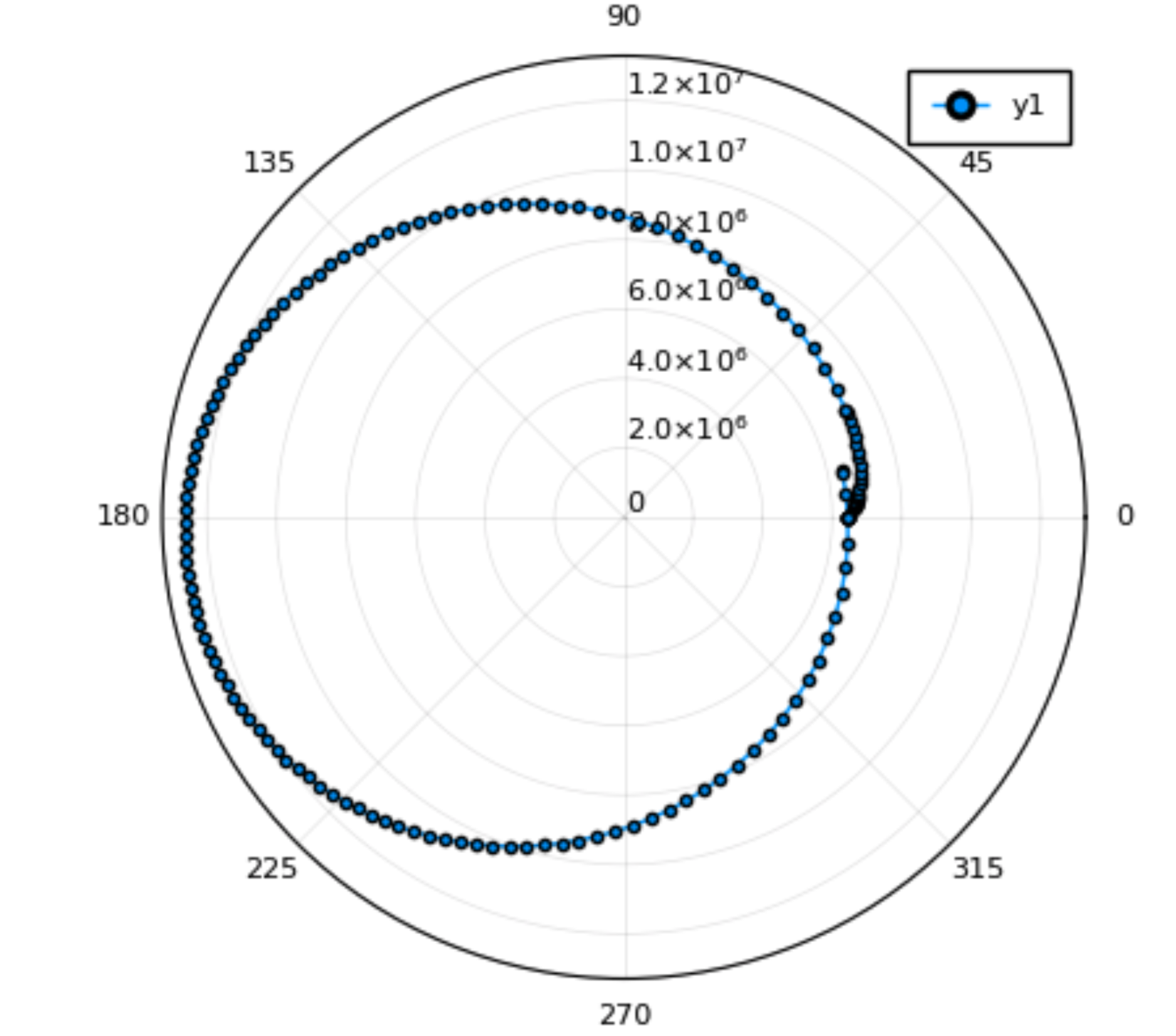
-
-
然后是坠落的情况,由于其没有进入第一宇宙速度而坠落了
parameter value \(m_{rocket}\) 33800.0 \(m_{fuel1}\) 367500.0 \(m_{fuel2}\) 140000.0 \(t_{inject_1}\) 330.0 \(t_{inject_2}\) 720.0 \(v_{limit1}\) 100.0 \(v_{limit2}\) 400.0 \(v_{limit3}\) 6000.0 \(p_{e}\) 9.7\(\times\)1000000 \(massflow\) 273.6 \(Area_{chamber}\) pi \(\times\) 0.92^2 \(u_e\) 3413 \(T1\) 6806000 \(T2\) 934000 \(R0\) 6400000.0 \(k_{aero}\) 3.7^2 \(\times\)0.25\(\times\) 1/2 \(v_0\) 10.0 \(theta0\) 6