Understanding Convolutional Neural Networks with A Mathematical Model
CNN(Convoulutional Neural Network)是一种受人眼识别物体的过程启发而实现的架构,其中比较有名的网络架构为Yann Lecun提出的LeNet-5和Hinton提出的AlexNet,平时我们使用CNN的时候都是一种基于感觉的来控制网络的结构,分配超参数,但是这样在模型规模越来越大的今天,这条路是会逐渐走到头的,因此,我们应该想办法对CNN进行一下Mathematical的分析。
CNN,设计上是为了去捕捉一幅图片的一个个像素之间关系的模型,因此,很容易的基于经验推出,More layer,More capability,似乎更深的网络就成了深度网络的银弹,但是在实践中,到了一定的深度后,网络的能力反而开始走下坡路了
The proposal of problem
而在 Understanding Convolutional Neural Networks with A Mathematical Model 一文中,C.-C. Jay Kuo 教授提出了一种方法去一部分程度上更好的理解CNN的结构,并在文章中提出了两个设计的原则方法的解释:
- 为什么CNN中,在卷积运算后需要设计非线性激活函数
- 为什么CNN中,堆砌复数的卷积层会取得更好的效果
RECOS Model
在文中,其实这两个问题是有相互依存关系的,但是为了推导,还是先叙述第一个问题,在叙述之前,需要先介绍作者在文中提出的RECOS(REctified COrrelations on a Sphere)模型:
想法是这样的,如果现在单位球面上的点,需要去做分类的话,需要找一个度量来确定点和点之间的关系,自然的想到,单位球面上的测地距离是一种很好的度量。如果通过测地距离来对于球面上的点来做分类的话,在其中夹角 \(0 \leq \mid \theta \mid \leq 90\) 的时候,夹角(相似度)和测度距离是等价的,此时 \(cos(\theta)\) 是单调减少且恒正的:
\[\theta(x_i,x_j)=arccos(x_i^Tx_j)\]但是当夹角 \(90 < \mid \theta \mid \leq 180\) 的时候,此时 \(cos(\theta)\) 是单调减少但是恒负的,这样就不适合用来做度量了,如下图所示,在 \(\theta\) 居于合理的区间内的时候,相关度越大,测地距离越短,但是到了 \(cos\theta\) 为负的时候,这不适合用作度量。
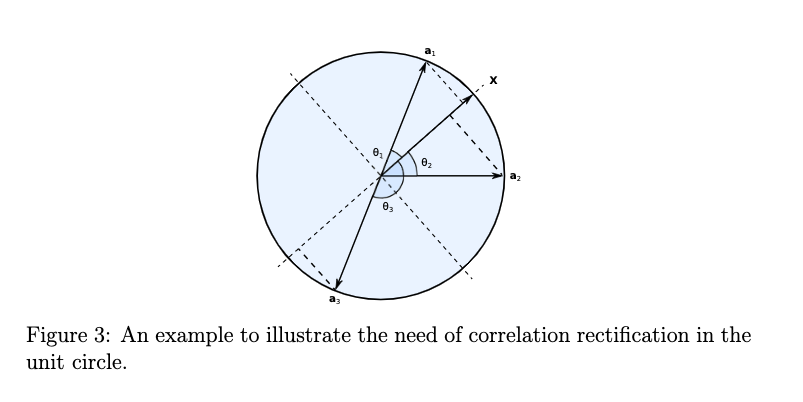
当 \(\theta = 180\) 的时候,在某些意义上,\(x,a_3\)之间的关系非常强,如下图中的黑猫,白猫所示,但是两点间是单位球上最大的测地距离:

这样显然是不好的咯,比如系统是两层的这样的RECOS模型,第二层的输入是第一层的输出,那么对于系统来说,他是无法分辨两层的这样的情况的:
- 第一层给出正反应,第二层的anchor是负的
- 第一层给出负反应,第二层的anchor是正的
这样两层最后的输出的都是负的,因此需要解决这个问题,一种想法就是把负的输出,压缩到零(接近0),那这样就不会造成歧义。
那么从某种意义上来说,卷积层,如果把filter的参数固定以后,把 filters 想象成之前系统中的 \(a_i\),然后 input 的图像是 \(x\) 的话,那么一层有 \(K\) 个filter,那这样定义,卷积层等价于一个RECOS层。
Nonlinear Activation Function
于是可以开始叙述关于非线性激活函数整流的重要性,以LeNEt-5为例,在mnist上训练完的LeNet-5可以倒倒98.94%的正确率,但是相反的,如果把mnist的像素图取逆,则会使得模型的正确率下降到30%左右。这样显然是有问题的,解决方法是,对于逆的像素,我们把第一层的卷积层参数取逆即可,但是这样对于原来的mnist识别率又会掉下去。于是我们可以通过RELU的非线性激活函数来解决这个问题,以此来验证非线性操作的重要性。
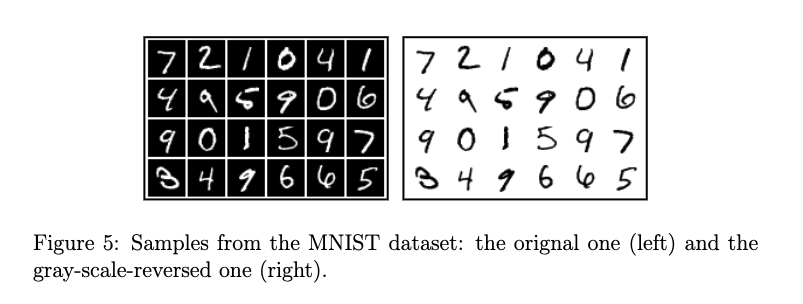
输入图像 \(x\), 已知训练完成的LeNet-5的第一层参数为 \(a_k\), \(y=(y_1,...,y_n)\)
\[y_k(x,a_k)=\max(0,a^T_kx)\]考虑到,对数据常做的pre-process,考虑平移的单位球面:
\[S_{\mu}=\left\{\mathbf{x} \mid\|\mathbf{x}-\mu \mathbf{1}\|=\left[\sum_{n=1}^{N}\left(x_{n}-\mu\right)^{2}\right]^{1 / 2}=1\right\}\\\]其中的 \(\mu = \frac{1}{N}\sum_{i=1}^N x_n\)
于是对 \(S_{\mu}\)有 \(y_k(x-\mu I,a_k)=Rec(a^T_kx-\mu\sum_{i=1}^N a_{k,n})\)
如果定义 \(x'=(\mu,x_1,...,x_N)^T,a'_k=(\sum_{i=1}^N a_{k,n},a_{k,1},...)\),并且考虑到更一般的归一化问题的话,就可以有:
\[y_{k}\left(\mathbf{x}^{\prime \prime}, \mathbf{a}_{k}^{\prime \prime}\right)=\left\|\mathbf{x}^{\prime \prime}\right\|\left\|\mathbf{a}^{\prime \prime}_{k}\right\| \operatorname{Rec}\left(\mathbf{a}_{k}^{\prime T} \mathbf{x}^{\prime}\right)\] \[x'=\frac{x''}{\|x''\|}, a_k'=\frac{a_k''}{\|a_k''\|}\]那么对于之前取逆的输入,\(x_r=255 \mathbf{1}-\mathbf{x}\), \(a_{r,k}=-a_k\)
\[\begin{aligned} y_{k}\left(\mathbf{x}_{r}-\mu_{r} \mathbf{1}, \mathbf{a}_{r, k}\right) &=y_{k}\left(255 \mathbf{1}-\mathbf{x}-(255-\mu) \mathbf{1},-\mathbf{a}_{k}\right) \\ &=y_{k}\left(\mathbf{x}-\mu \mathbf{1}, \mathbf{a}_{k}\right) \end{aligned}\]实际上,\(a_k\) 的取值,一般对应着 \(k\) 个纹理模式,而多加一倍的逆的anchor以及整流函数的存在,使得同一层layer的识别能力上升了
Advantages of Cascaded Layers
之前给出了非线性整流函数的必要性,那部分里面其实已经提及了一部分网络设计中丰富的feature map的必要性,当然可以说,没有这么理想的,怎么会做到完全取逆什么的,实际上,堆砌的feature数量越多,即同一层里面的feature extractor越多,网络捕捉信息的能力越强。
而另一种提升方法,就是堆砌更多的层数,尽管从维度上来说,端到端的CNN的输入输出维不会随着网络的变深而变化,但是通过更多的层数,可以使得捕捉到的信息更加的丰富。
Two Layer One-to-One Cascade
\[A=[a_1,....a_K],B=[b_1,...,b_L]\]对于输入的图片 \(x\), \(y=A^Tx,z=B^Ty\)
\[z=B^Ty=B^TA^Tx=C^Tx\]通过把 \(x\)做分解 \(x=\sum_{i=1}^N x_{n}e_n\)
就有了anchor位置向量 \(\alpha_n=A^Te_n\)
\[c_{n,l}=\alpha_n^Tb_l\]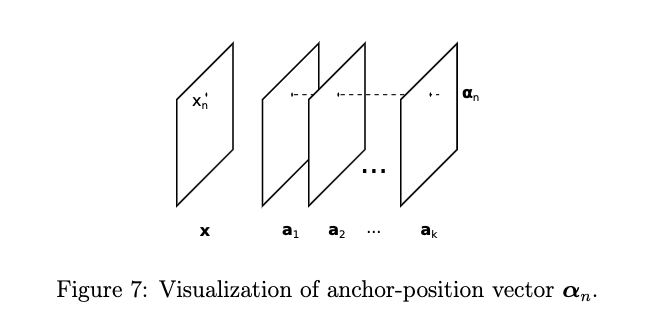
One Layer System
\[D=[d_1,...,d_L]\]对于输入的图片 \(x\), \(z=D^Tx\)
这两种系统,D 承担了A,B两部分的功能, A 和 D 都很容易学习到全局的模式表示,但是更深的网络,由于有 B 的存在,就可以利用之前由anchor位置向量捕捉到位置相关的信息。

再加入了背景信息的mnist中,在重新训练后,正确率相差无几,这是由于背景信息没有被第一层的anchor向量捕捉到,而传入第二层的位置信息全是关于mnist的手写体的,于是神经网络就可以专注于手写体,因此正确率相差不会很大。这是浅层的网络做不到的。
Reference
[1] C.-C. Jay Kuo Understanding Convolutional Neural Networks with A Mathematical Model