• Introduction
• Single Image Super Resolution Models
  • Prediction Model
    • Interpolation Kernels
    • Nearest Neighbor
    • Bilinear
    • Bicubic
  • Patch-based Model
    • Sparse Representation Super-Resolution
    • Super Resolution Convolutional Neural Network
  • 参考文献

深度学习在计算机视觉大成功的当下，我们也需要严格审慎的看待深度学习的各项应用，与handcraft的传统方法在特定问题上的比较，优化目标和现实目标的配准，以及深度学习超分辨率模型内部问题的解析。这篇文章主要关注超分辨率（SR）中单图像超分辨率（SISR）中Patch based model的应用，有前深度学习时代的SRSR(Super Resolution Via Sparse Representation)和SRCNN(Super Resolution Convolutional Nerual Network)，然后是基于统计模型的SRGAN和其加强版SRGAN

Introduction

这篇文章主要注重于Statistical Model中的CNN和GAN在SR问题上的应用，当然会涉及一部分用来做SR的传统插值算法，比如基于Prediction Models的bilinear, bicubic。

SR(Super-resolution)，其实是很大的一个研究方向，本文中注重于空间域中的SISR(SIngle Image Super-Resolution)，即单图像超分辨率，SISR不考虑视频的每帧图片之前的互信息，相反的，只能利用单图像的信息和模型中携带的先验信息（prior）做超分辨率。SISR，可以说是一个很有意思且有应用空间的的课题。

这个问题，目标描述起来很实在的，就是所谓把低分辨率（LR）的图像变成高分辨率（HR）的图像，同时保证HR图像有不错的观感。很自然的可以想到，生活中会存在一些图片，由于传送过程中的有损压缩，我们看到时是低分辨率的，人看起来非常的不愉悦，就比如要想办法把右边的莲花恢复成左边那样的，这是很有价值的应用。

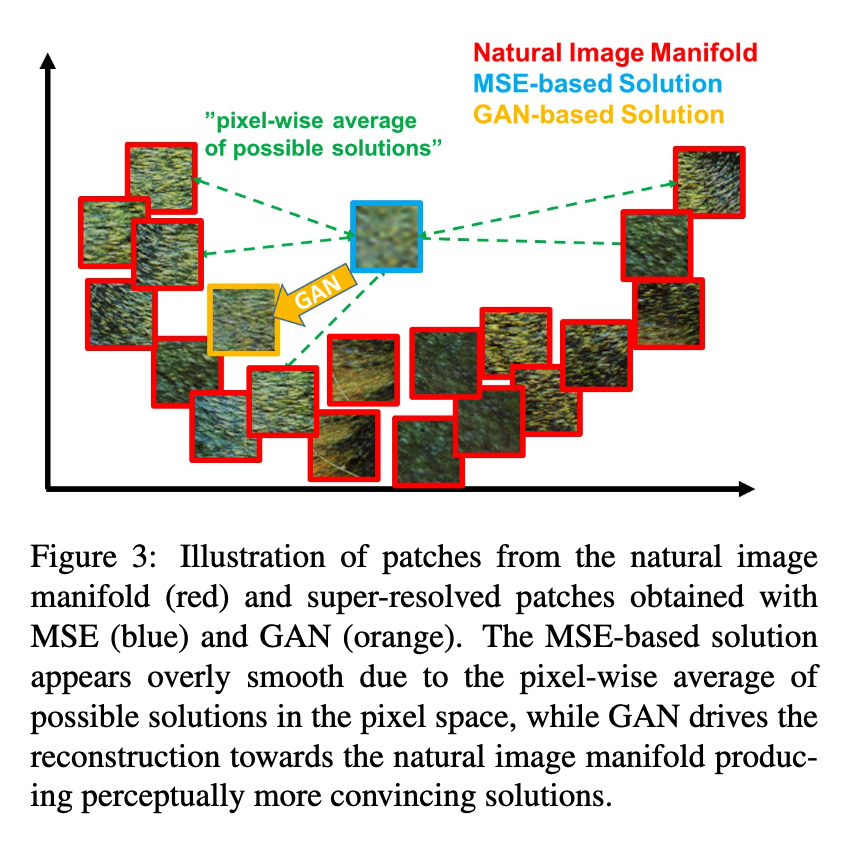
SR问题的有趣之处，也在于这一点，从HR到LR很容易，有各种算法来实现，但是反过来，从LR空间映回去到HR空间的映射，不仅映射本身很难处理，而且这个问题是病态问题，基于同一个比如MSE的误差，其实一个LR的图片，在HR空间里可能对应着一个流形，这就引出了问题，视觉上的最好，不应当是这样一个HR空间中的流形上的每个点，而是个别的，要找到一个优化目标，能够量化所谓看起来自然这种很抽象的命题，而且甚至每个观察者都持有不一样的评判标准，建立这个优化目标非常的困难。

Single Image Super Resolution Models

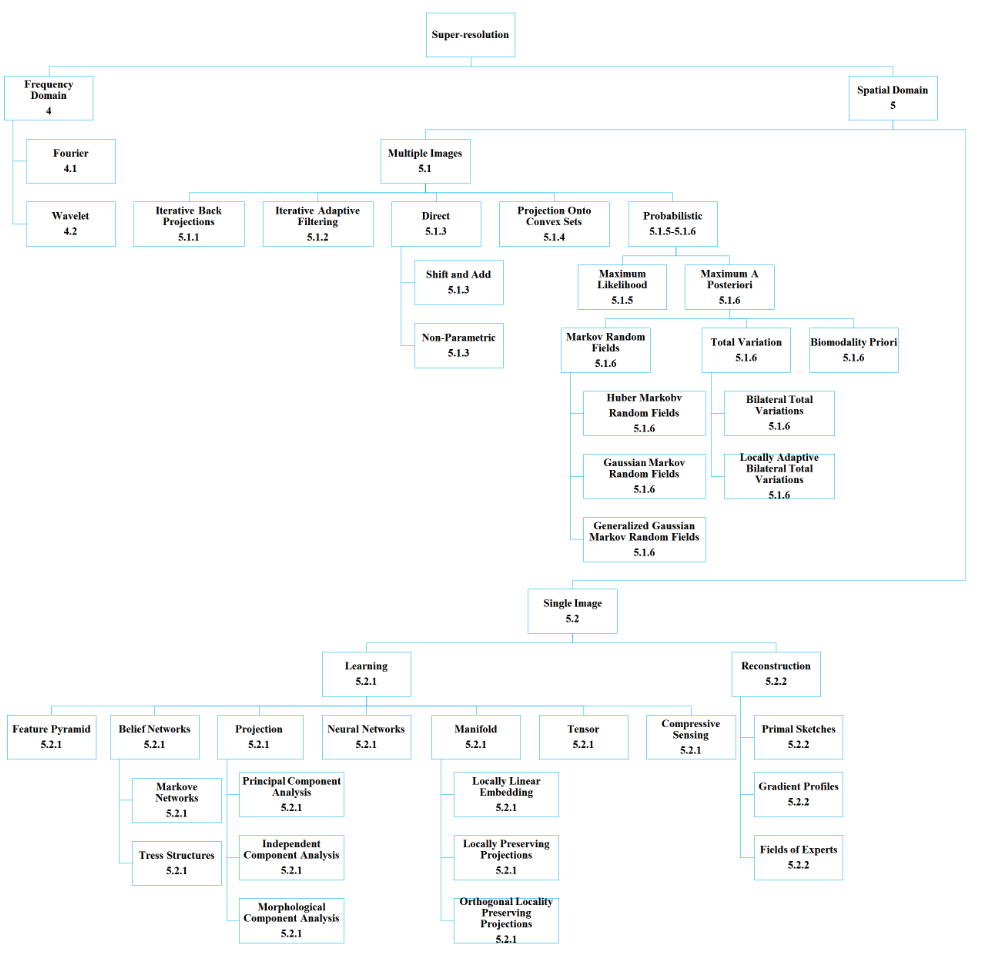
在比较传统的观点下，根据不同的图像先验（Image Prior）使用方法，SISR模型是可以被分成prediction model，edge based methods，image statistical methods和 patch based（example-based）methods的。在其中，在神经网络方法提出前，patch based methods是SOTA。而后文中，SRDCN中证明了其本质就是patch based methods。

Prediction Model

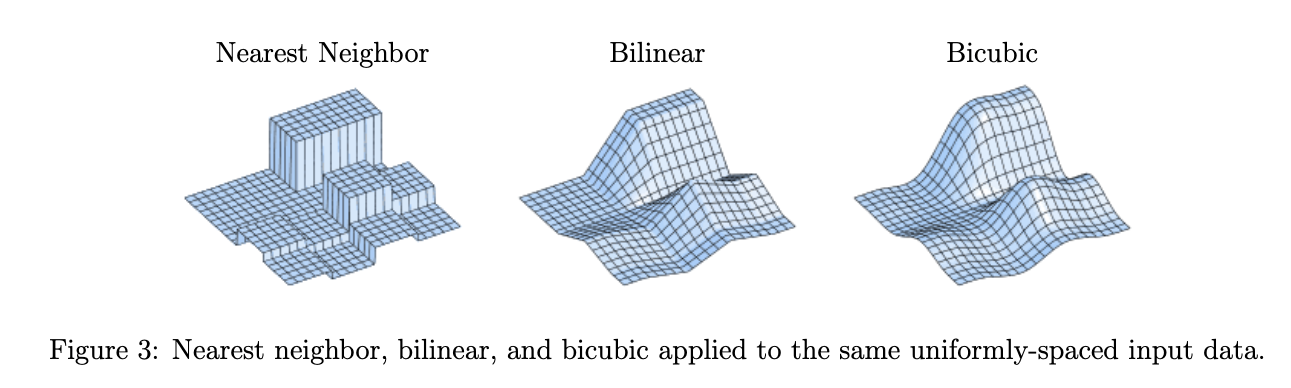
Prediction Model从Image Prior来看，是不使用数据集训练的，SR映射就是一个预先定义的数学公式，其中比较流行的方法就是bilinear, bicubic这样此类插值算法，由于这类插值算法通过在local pixel之间进行加权平均，他们的结果，会体现出比较好的像素光滑性（吐槽，视觉效果上，光滑大概是反而不好的，么得对比度）

但是要讲这两个算法前，先要声明插值核（Interpolation Kernels）和最近邻插值算法（Nearest Neighbor）

Interpolation Kernels

在Linear Methods for Image Interpolation一文中，给出了如下的Prediction Model的形式：

\(v_{m,n}\)是所谓的采样图像，是以pixel的格式给出的，那么插值的目的其实是找到\(v\)的潜在函数

\[v_{m,n}=u(m,n)\;for\;all\;m,n \in Z\]

然后可以定义线性算子\(Z\)把\(v\)映射到\(Z(v)\)

1. \(S_{k,l}\)表示平移算子，平移不变性：\(Z\left(S_{k, l}(v)\right)(x, y)=Z(v)(x-k, y-l)\)
2. \(v^N\)表示v被限制在\(\{-N,...,N\}^2\)，局部性：\(Z(v)(x, y)=\lim_{N\to\infty}Z(v^N)(x, y)\)

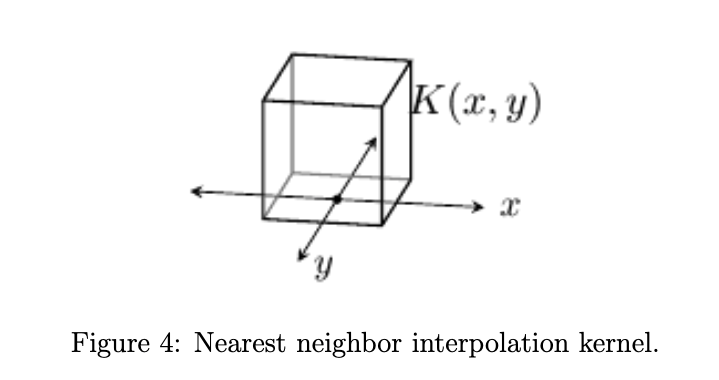
那么在这样的条件下，如果有一个线性的，平移不变的，局部的算子\(Z\)，可以找到插值核函数\(K\in L^1\) \(Z(v)(x, y)=\sum_{m,n \in Z} v_{m,n}K(x-m,y-n)\) 一般在\(K\)上，还会被设计有一些很好的性质，比如$K$被设计成一个张量积，\(K(x,y)=K_1(x)K_2(y)\)，其中\(K_1\)是对称的

Nearest Neighbor

最近邻插值，很直白的说明了就是用附近的pixel进行插值： \(u(x,y)=v_{[x],[y]}\) $[.]$就表示最邻近的位置，也由此，一般最邻近插值也被叫做“像素复制” \(K(x,y)=K_1(x)K_1(y);\;K_1(t)=\left\{ \begin{aligned} 1 &\;\;\;if\;t\;is\;nearest\;neighbor \;\;or\;t\in[-\frac{1}{2},\frac{1}{2}] \\ 0 &\;\;\;otherwise\\ \end{aligned} \right.\) 最近邻插值的插值核如下，非常的“最近邻“

Bilinear

双线性插值是一个连续函数，其中的：\(\lfloor.\rfloor\)表示floor function，而$=x-\lfloor x\rfloor$，具体形式如下： $$ \begin{aligned} u(x, y) &=(1-\langle x\rangle)(1-\langle y\rangle) v_{\lfloor x\rfloor,\lfloor y\rfloor}+\langle x\rangle(1-\langle y\rangle) v_{\lfloor x\rfloor+1,\lfloor y\rfloor} \left.\\+(1-\langle x\rangle)\langle y\rangle v_{\lfloor x\rfloor,\lfloor y\rfloor+1}+\langle x\rangle\langle y\rangle v_{\lfloor x\rfloor+1,\lfloor y\rfloor+1}+1\right\rangle \end{aligned} $$ 其插值核形式为： $$ K(x,y)=K_1(x)K_1(y), K_1(t)=(1-|t|)^+=max(1-|t|,0) $$

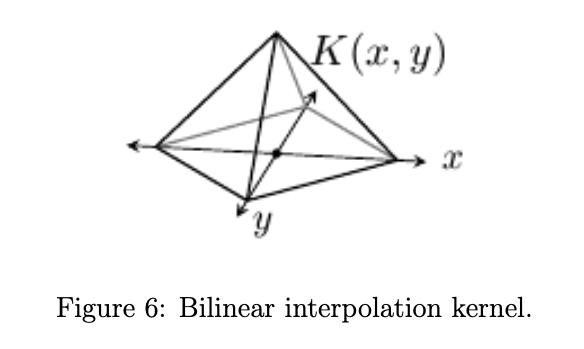
在每个\([m,m+1]\times[n,n+1]\)内，插值都是附近的4个pixel的凸组合（如上图），这样的话，插值至少不会产生异常的over/undershoot至少在视觉上不突兀；其次双线性有仿射不变性：\(v_{m,n}=am+bn+c\)，则$u(x,y)=ax+by+c$

Bicubic

双三次使用如下的插值核，其中\(\alpha\)是一个自由参数： \(K(x,y)=K_1(x)K_1(y),\;K_{1}(t)=\left\{\begin{array}{ll} (\alpha+2)|t|^{3}-(\alpha+3)|t|^{2}+1 & \text { if }|t| \leq 1 \\ \alpha|t|^{3}-5 \alpha|t|^{2}+8 \alpha|t|-4 \alpha & \text { if } 1<|t|<2 \\ 0 & \text { otherwise } \end{array}\right.\) 下图的插值核使用的是\(\alpha=-0.5\)的参数

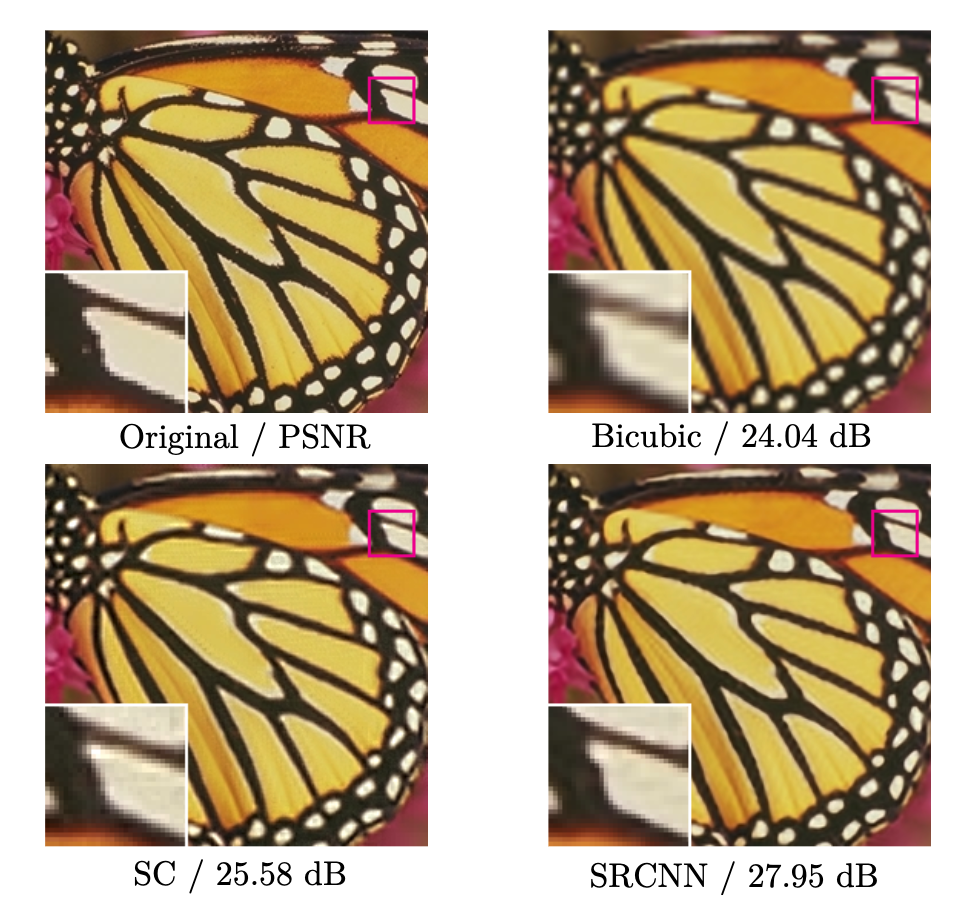
可以看到的是，无论何种形式的Prediction Model，都没有一个learning的过程，真正做到了可理解的Prior利用过程；而是直接利用既有的所谓积累下来经验，去估计一个最好的插值核去进行超分辨率，甚至有些模型是没有调整的空间的。（胡言乱语：这样的话，信息量被高度压缩在一个很简单的经验公式里，大部分情况下，在效果上肯定会比把Prior嵌入到比较大的结构，无论是字典或者是神经网络，就比如下图，bicubic比SC模型和SRCNN效果上会差）

Patch-based Model

这里主要研究SRCNN模型，但是首先需要由通过稀疏表示的patch based模型做引子，在patch-based model研究历史上，Sparse Representation Super-Resolution是非常重要的起承转合的方法，为后来GPU算力大爆发时，SRCNN的出现做了铺垫。

Patch based的想法是，把大的图像切割成一块块有相互覆盖的patches，然后在每个patch上，完成HR后，再把patches一块块拼接起来，当然其中一步步都要满足一些约束，使得生成的图片质量更好。

Sparse Representation Super-Resolution

SRCNN的话，和以稀疏编码为基础的representative external example-based SR有很深的关系，因此，为了理解SRCNN的patch based，应该先理解representative external example-based SR。下面以Image Super-Resolution via Sparse Representation中的稀疏表示方法为例，下面简称该模型SRSR（Sparse Representation Super-Resolution）

SRSR的基本想法就是把LR图像输入后，切割成一份份patches，然后在每个patch上利用预训练的字典做稀疏表示，然后再利用HR图像预训练的字典，做对应的HR图像的稀疏表示，然后再把这一片片的patches贴回HR图像，再在整份图像这样的全局的角度下，做一些优化，就又LR图像恢复出了HR图像。

SRSR的pipeline中比较算力负担低的方案如下：

为了预训练字典，则SRSR的模型细节具体如下：

Symbol	Mean
\(X\)	High Res Image
\(Y\)	Corresponding Low Res Image of \(X\)
\(x\)	Patch of \(X\)
\(y\)	Patch of \(Y\)
\(D_h,D_l\)	Corresponding dictionary of HR&LR patch
\(\alpha\)	Sparse DIctionary Representaion of patch

• 通过下采样矩阵 \(S\) 和模糊滤波器 \(H\)来算出对应的 \(Y\)

\[Y=SHX\]

对于每个patch \(y\) ,去寻找对应的稀疏表示 \(\alpha\) ，\(F\) 是一个特征提取器（一般采用高通滤波器，因为人眼对于高 频信息更加敏感，因此在视觉上，复建的消费会更好），满足：

\[\begin{aligned} \min \|\boldsymbol{\alpha}\|_{0} \;\; \text { s.t. } \left\|F \boldsymbol{D}_{l} \boldsymbol{\alpha}-F \boldsymbol{y}\right\|_{2}^{2} \leq \epsilon \end{aligned}\]

但是由于0-范数难以优化，选择1-范数做近似：

\[\begin{array}{c||c} \min_{\alpha} \|\boldsymbol{\alpha}\|_{1} \;\; \text { s.t. } \left\|F \boldsymbol{D}_{l} \boldsymbol{\alpha}-F \boldsymbol{y}\right\|_{2}^{2} \leq \epsilon \end{array}\]

由拉格朗日乘子法提供了等价的形式，其中 \(\lambda\) 用来平衡稀疏性和对 \( y\)的近似的准确度：

\[\begin{array}{c||c} \min \lambda\|\boldsymbol{\alpha}\|_{1} + \left\|F \boldsymbol{D}_{l} \boldsymbol{\alpha}-F \boldsymbol{y}\right\|_{2}^{2} \end{array}\]

上述算法是对于单个的局部的patch来说的，但是复建出的图像，需要在比较大的局部尺度内有比较好的光滑性，因此规定 \(\omega\) 是上一个复建的patch的结果， 而 \(P\) 提取了复建patch间重叠的区域，满足：

\[\begin{array}{c||c} \min \|\boldsymbol{\alpha}\|_{1} \text { s.t. } & \left\|F \boldsymbol{D}_{l} \boldsymbol{\alpha}-F \boldsymbol{y}\right\|_{2}^{2} \leq \epsilon_{1} \\ & \left\|P \boldsymbol{D}_{h} \boldsymbol{\alpha}-\boldsymbol{w}\right\|_{2}^{2} \leq \epsilon_{2} \end{array}\]

而同样的，有等价形式:

\[\begin{array}{c||c} \min_{\alpha} \lambda\|\boldsymbol{\alpha}\|_{1} + \left\| \tilde{\boldsymbol{D}} \boldsymbol{\alpha}- \tilde{\boldsymbol{y}}\right\|_{2}^{2} \tilde{\boldsymbol{D}}=\left[\begin{array}{c} F \boldsymbol{D}_{l} \\ \beta P \boldsymbol{D}_{h} \end{array}\right] \text { and } \tilde{\boldsymbol{y}}=\left[\begin{array}{l} F \boldsymbol{y} \\ \beta \boldsymbol{w} \end{array}\right] \end{array}\]

同时之前的约束中，并没有要求 \(F \boldsymbol{D}_{l}\) 和 \(\alpha\) 之间的相似度， 为了消除由此导致的差异，把之前的得到的复建图像 \(X_0\) 加上约束：

\[\begin{aligned} \boldsymbol{X}^{*}= argmin_{X} \|SH\boldsymbol{X}-\boldsymbol{Y}\|_{2}^{2} + c\|\boldsymbol{X}-\boldsymbol{X_0}\|_{2}^{2} \end{aligned}\]

然后上式提供解:

\[\begin{align} \boldsymbol{X}_{t+1}=\boldsymbol{X}_{t}+\nu\left[H^{T} S^{T}\left(\boldsymbol{Y}-S H \boldsymbol{X}_{t}\right)+c\left(X-X_{0}\right)\right] \end{align}\]

• 预训练的字典 \(D\) 是pipeline的重要组成部分，字典一般通过一个数据集\(X=\{x_1,x_2,...,x_t\}\)，在要求尽可能小的字典的约束下，有如下优化目标：

\[\begin{aligned} \boldsymbol{D}=& \arg \min _{\boldsymbol{D}, \boldsymbol{Z}}\|X-\boldsymbol{D} Z\|_{2}^{2}+\lambda\|Z\|_{1} \\ & \text { s.t. }\left\|D_{i}\right\|_{2}^{2} \leq 1, i=1,2, \ldots, K \end{aligned}\]

然后按照如下算法训练基于 \(X\) 的字典

而在SRSR中，HR图像和LR图像是对于两个字典的，并且有数据集\(X^h,Y^l\)

对于HR图像而言，\(\boldsymbol{D_h}= \arg \min _{\{\boldsymbol{D_h}, \boldsymbol{Z}\}}\|X^h-\boldsymbol{D_h} Z\|_{2}^{2}+\lambda\|Z\|_{1}\)

而对于LR图像而言，\(\boldsymbol{D_l}= \arg \min _{\{\boldsymbol{D_l}, \boldsymbol{Z}\}}\|Y^l-\boldsymbol{D_l} Z\|_{2}^{2}+\lambda\|Z\|_{1}\)

为了同步优化，组合一下有优化目标：

\[min_{\{\boldsymbol{D_h},\boldsymbol{D_l},Z\}}\frac{1}{N}\|X^h-\boldsymbol{D_h} Z\|_{2}^{2}+\frac{1}{M}\|Y^l-\boldsymbol{D_l} Z\|_{2}^{2}+\lambda(\frac{1}{M}+\frac{1}{M})\|Z\|_{1}\]

而经过训练的字典内部的信息可视化后如下，确实有点CNN Visualization卷积那味啊，后面在SRCNN中也将证 明其等价性。

Super Resolution Convolutional Neural Network

SRCNN

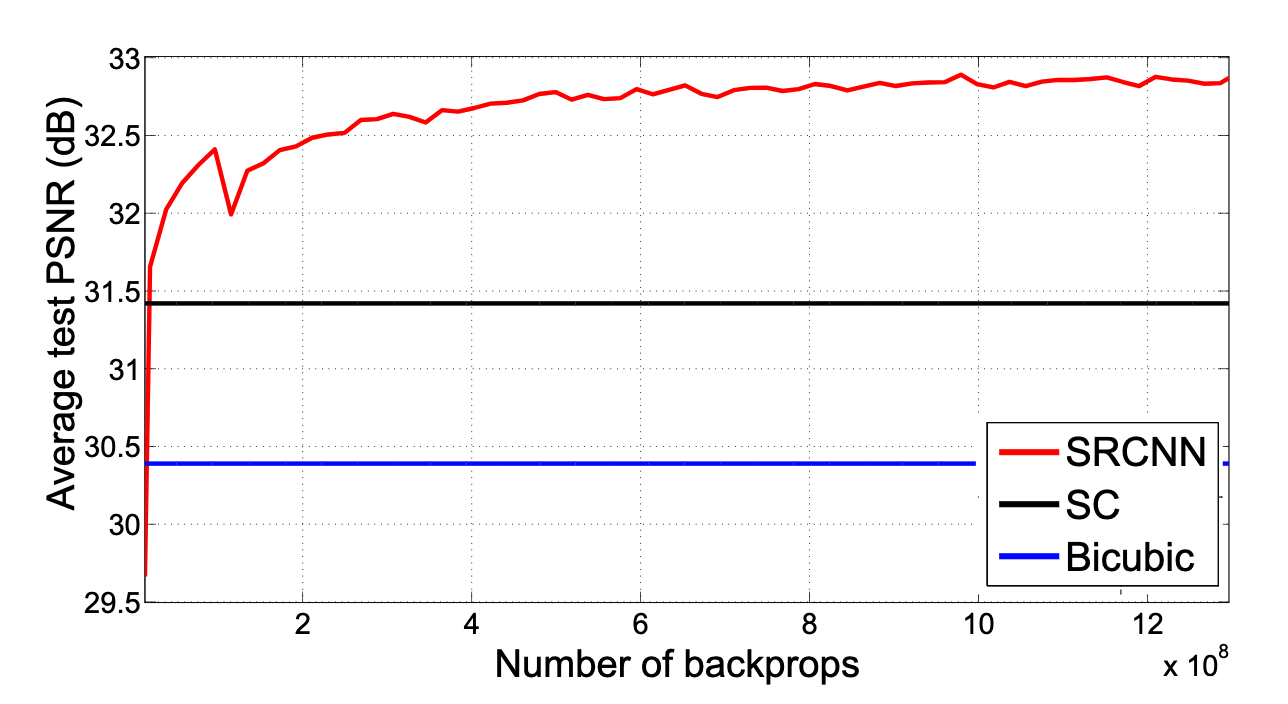
深度学习的端到端的性质，使得优化过程空前的简单；而合理利用GPU的性质，尽管在参数数量上看似会比传统方法多几个量级，却得益于前向传播算法，在速度上最终与传统方法差不多；在经过合理的数据集训练后，在效果上完全可以超过传统方法。妙哉妙哉

在Image Super-Resolution Using Deep Convolutional Networks一文中，提出的SRCNN，在经过适当的训练之后，就达到了当时的SOTA水准

Symbol	Mean
\(X\)	Ground Truth
\(Y\)	Corresponding Low Res Image of \(X\)
\(F\)	Interpolation Map
\(W_i\)	Filter of i th layer
\(B_i\)	Bias of i th layer
*	Convolution Operation

SRCNN在结构上很mind-simplicity，而在设计上采用全卷积的设计。在功能划分上，SRCNN总归分成了三部分：

• Patch提取和表示: \(F_1(Y) = max(0,W_1*Y+B_1)\) \(W_1\) 对应 \(n_1\) 个 filter，尺寸为 \((f_1,f_1,c)\)

  \(B_2\) 为 \(n_2\) 个feature map的bias

  这一层把输入的被双三次插值的LR图像，用卷积的方式映射成 $n_1$ 的特征

• 非线性映射 \(F_2(Y) = max(0,W_2*F_1(Y)+B_2)\) \(W_2\) 对应 \(n_2\) 个 filter，尺寸为 \((f_2,f_2,n_1)\)

  \(B_3\) 为 \(n_3\) 个feature map的bias

  第一层提取的 \(n_1$v 维的特征，映射到\)n_2$v 维，是把 \(3\times3\) 的patch做非线性映射，映射的结果本质上是HR图像的表示，后面会被用作复建

• 复建 \(F(Y) = W_3*F_2(Y)+B_3\) \(W_3\)对应 \(n_2\) 个 filter，尺寸为 \((f_2,f_2,c)\)

  一般方法中，复建往往对于这平均滤波器，而复建层的卷积也有类似的效果。

  那训练的目标函数很简单： \(\mathbf{L}(\theta) = \frac{1}{n}\sum_{i=1}^n \left\| F(\mathbf{Y_i};\theta)-\mathbf{X_i} \right\|\) 而SRCNN的总体结构如下图所示，每层的运算都是卷积，因此硬件上可以给出支持使得模型运算加速：

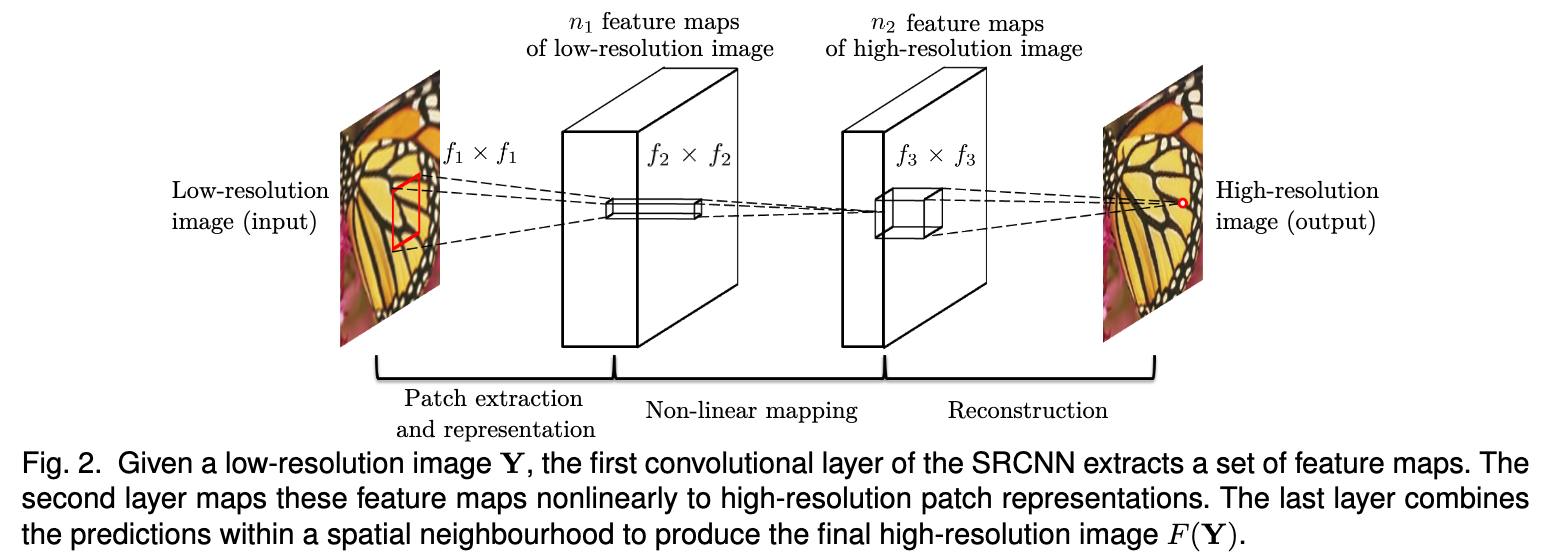
• 稀疏编码Patch based模型和SRCNN的等价性

  Patch提取和表示层中，对应稀疏编码方法的第一部分，是把LR图片进行编码，那么如果字典的原子数目是 \(n_1\) ，那么稀疏编码器所做的事情和卷积是一致的，就是把 \(n_1\) 个线性的 \((f_1,f_1)\) 滤波器用上去，和SRCNN的第一部分是一致的，就像一个\(n_1\) 维的特征表示，对应了就是稀疏表示（稀疏性成疑？，可能在网络训练过程中，通过特殊的激活函数或者参数正则化技术，可以对局部几个的feature（atom）响应比较好？）

  非线性映射层中，在稀疏编码器解出了LR空间中的图片的稀疏表示上，对其做一些非线性的优化，使得在HR空间中用相应的稀疏表示复建的图像更加视觉上观感好，这对应中间的非线性映射层。当然这里运算上会不太一样，这部分在SRCNN中仍然是前向传播的，而在SRSR中，这部分的是对于优化目标函数做梯度下降。

  而最后的复建层中，稀疏编码其利用HR空间中的字典，和解得的稀疏表示，恢复出相应的HR图片，具体的来说，就是把图片按照相应位置贴上去，patch间重复的部分做平均，这和卷积中的average conv kernel是一样的。

  而在总体结构上来看，无论卷积神经网络做的事情，还是每个layer的效果，都是一致的。

  

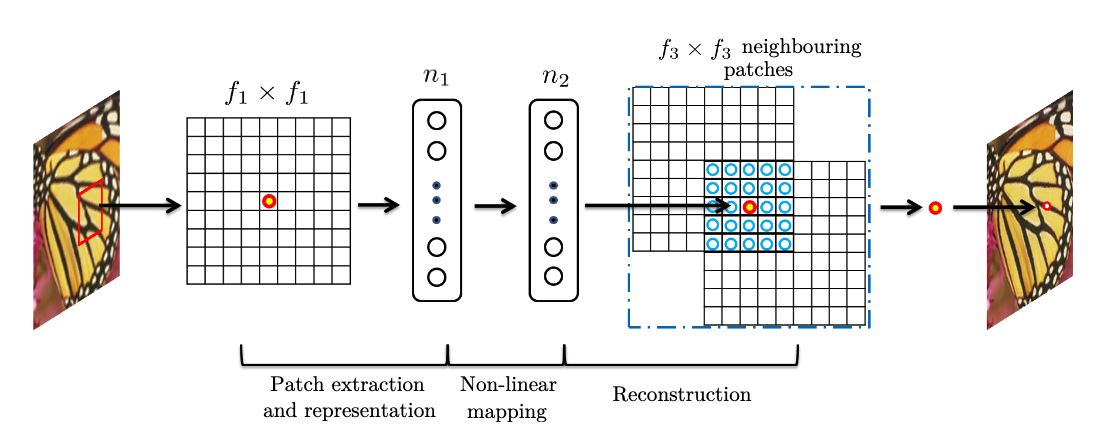
  参考文献

  [1] Pascal Getreuer Linear Methods for Image Interpolation

  [2] Chih-Yuan Yang , Chao Ma , and Ming-Hsuan Yang Single-Image Super-Resolution: A Benchmark

  [3] Jianchao Yang , John Wright , Thomas Huang , Yi Ma, Image Super- Resolution via Sparse Representation

  [4] Chao Dong, Chen Change Loy, Kaiming He, Xiaoou Tang Image Super- Resolution Using Deep Convolutional Networks

  [5] https://en.wikipedia.org/wiki/Image_scaling