Generative Model Part 0:Theoretical Basis of Generative Model
这篇文章终于可以开始写,想了很久的生成模型系列,在其中,主要研究的是基于一个隐空间的生成模型,其中笔者最喜欢的是 VAE 系列和 GAN 系列。但是这一篇中暂且不表这两种模型的具体问题,而是先研究一下生成模型的一些理论基础。
生成模型,简单来说,目的是去在高维空间 \(\chi\) 中,找到关于 \(X\) 的分布 \(P(X)\) 的分布,因为其中 \(X\) 的维度一般非常的高,其实是图像已经略显粗糙 \(Mnist\) 数据集,其每个像素图的尺寸也为 \(28 \times 28 = 784\) 维,从这个结果来看,直接去生成每个pixel,再组成一幅pixel image是反直觉的,对于人来说,在脑中构想一个 \(2\) ,似乎一般不用做到思考到独立的 \(784\) 维,而是思考一下笔画有多粗,笔画的角度大概多少,构型大概是怎么样的,那么很天然的,如果要去模仿人去写 \(2\) 的样子,就应当是从维度有一个远低于 \(784\) ,这个像素图原来的维度的空间,来生成的数字 \(2\),生成空间的隐空间,这样的想法就呼之欲出了
从隐空间的角度来说,生成模型所做的,就是去学习一个映射,把低维隐空间流形嵌入到高维的数据空间中的映射,在给定某些条件下,生成模型参数化了数据空间中的流形,通过 \(z \in Z\),和生成模型 \(f:Z \rightarrow \mathcal{X}\) ,去生成 \(x\in\mathcal{X}\)
\[\mathbf{x}=f(\mathbf{z})\]1. From Latent Space Geometry Point of View
隐空间,不能用欧氏距离去研究,这样有时候会导出和直觉相反的结果,还是以 \(Mnist\) 数据集为例:“如何定义两个字符之间的距离?”通过在像素意义下,\(d(\mathbf{z_1},\mathbf{z_2}) = \left\|f\left(\mathbf{z_1}\right)-f\left(\mathbf{z_2}\right)\right\|^{2}\),可以在数值上导出一个距离,但这样定义的距离有时和直觉上是相矛盾的(常识上),通过下面的例子来说明:
如下图所示,\(A,B\) 分别代表两种写法的字符 \(0\),而 \(C\) 代表字符 \(1\),计算像素意义上的距离的话,\(d(A,B) > d(B,C)\),这不合常识!因此为了研究隐空间,需要定义测地距离,如右图所示,在隐空间流形嵌入到数据空间后,图示两点之间的测地距离和欧式距离是不同的,这也是之前 \(M ni s t\) 的例子中,\(d(A,B) > d(B,C)\) 这样的现象出现的原因,而且在实验结果中,测地距离在很多问题中,确实更加的“符合常识”
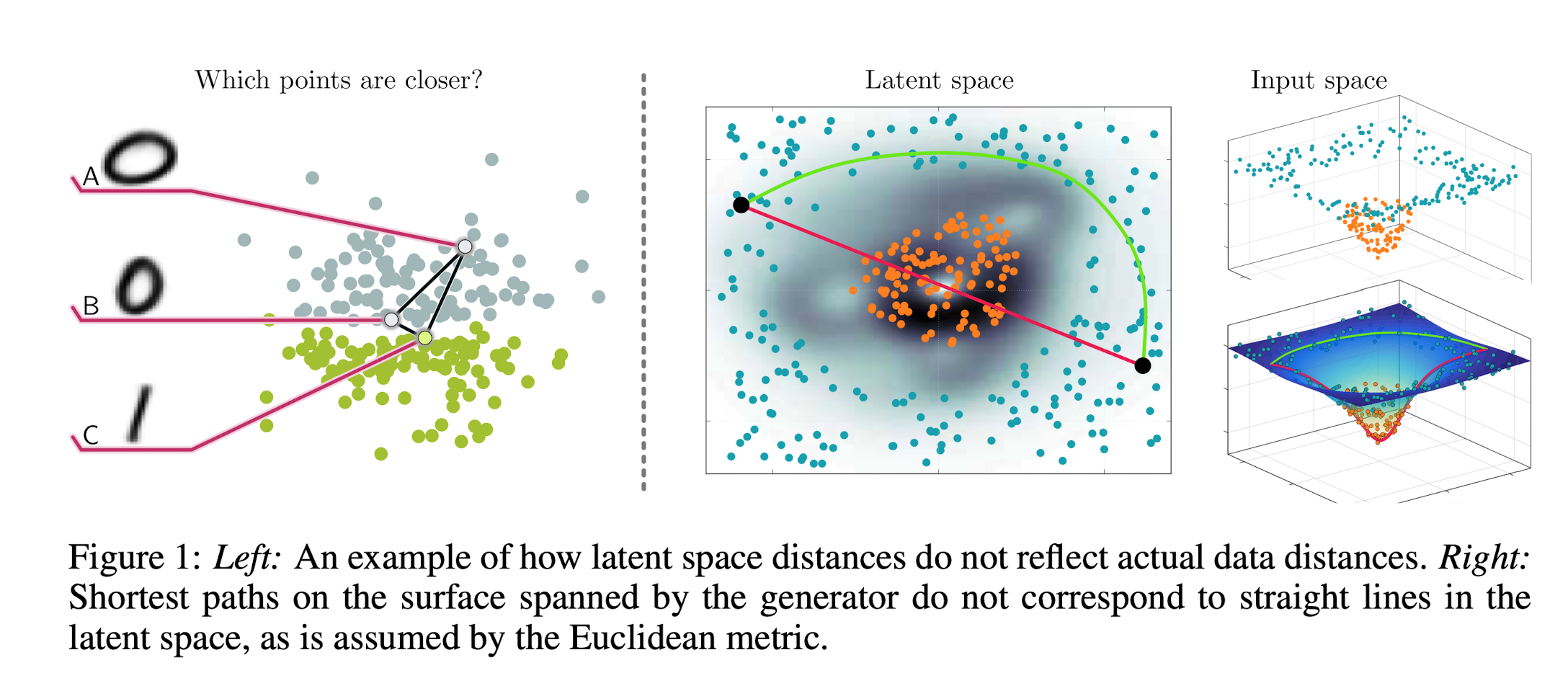
1.1. Shortest Path of Determinstic Generative Model
\(\mathbf{x}=f(\mathbf{z})\) 这样的模型,是确定的,没有噪声的结果,在此之上就可以得出一些关于测地距离的数值结果
那么就像上图所揭示的一样,测地距离,是一种 “locally” 距离,因此尝试通过两个极小量 \(\Delta \mathbf{z}_{1},\Delta \mathbf{z}_{2}\) 来定义距离,通过泰勒展开可以计算出:
\[\left\|f\left(\mathbf{z}+\Delta \mathbf{z}_{1}\right)-f\left(\mathbf{z}+\Delta \mathbf{z}_{2}\right)\right\|^{2} = \left(\Delta \mathbf{z}_{1}-\Delta \mathbf{z}_{2}\right)^{\top}\left(\mathbf{J}_{\mathbf{z}}^{\top} \mathbf{J}_{\mathbf{z}}\right)\left(\Delta \mathbf{z}_{1}-\Delta \mathbf{z}_{2}\right), \quad \mathbf{J}_{\mathbf{z}}=\left.\frac{\partial f}{\partial \mathbf{z}}\right|_{\mathbf{z}=\mathbf{z}}\]这符合局部的直觉,进一步说,随着 \(\mathbf{z}\) 的变化,测地距离相应的会发生变化(这由 \(\mathbf{z}\) 处的 Jocabian控制)
那么进一步的,有了局部的定义的话,希望能够“实用”的去算距离,现在把生成模型 \(\mathbf{x}=f(\mathbf{z})\) 看作一个空间中的光滑曲面,或者说数据空间 \(\mathcal{X}\) 中嵌入的光滑点集(光滑是为了后面能够直接使用已有的结论)
现有隐空间 \(\mathcal{Z}\) 中一条光滑曲线: \(\gamma_{t}:[0,1] \rightarrow \mathcal{Z}\) ,那么可以定义其长度:
\[\int_{0}^{1}\left\|\dot{\gamma}_{t}\right\| \mathrm{d} t = \int_{0}^{1}\left\|\mathrm{d} \gamma_{t} / \mathrm{d} t\right\| \mathrm{d} t\]再进一步把光滑曲线映射到数据空间 \(\mathcal{X}\),一样的就有长度:
\[\text { Length }\left[f\left(\boldsymbol{\gamma}_{t}\right)\right]=\int_{0}^{1}\left\|\dot{f}\left(\boldsymbol{\gamma}_{t}\right)\right\| \mathrm{d} t=\int_{0}^{1}\left\|\mathbf{J}_{\boldsymbol{\gamma}_{t}} \dot{\boldsymbol{\gamma}}_{t}\right\| \mathrm{d} t, \quad \mathbf{J}_{\boldsymbol{\gamma}_{t}}=\left.\frac{\partial f}{\partial \mathbf{z}}\right|_{\mathbf{z}=\boldsymbol{\gamma}_{t}}\]为了之后进一步考察流形 \(\mathbf{x}=f(\mathbf{z})\) 性质,考虑变换:
\[\left\|\mathbf{J}_{\gamma} \dot{\gamma}\right\|= \sqrt{\left(\mathbf{J}_{\gamma} \dot{\gamma}\right)^{\top}\left(\mathbf{J}_{\gamma} \dot{\gamma}\right)}= \sqrt{\dot{\gamma}^{\top}\left(\mathbf{J}_{\gamma}^{\top} \mathbf{J}_{\gamma}\right) \dot{\gamma}}= \sqrt{\dot{\gamma}^{\top} \mathbf{M}_{\gamma} \dot{\gamma}}\]这样比起之前没什么特征的 \(\dot{\gamma}_{t}\),有了对称正定矩阵 \(\mathbf{M}_{\boldsymbol{\gamma}}=\mathbf{J}_{\boldsymbol{\gamma}}^{\boldsymbol{\top}} \mathbf{J}_{\boldsymbol{\gamma}}\) 可以用来考察流形的性质
\(\mathbf{M}_{\boldsymbol{\gamma}}=\mathbf{J}_{\boldsymbol{\gamma}}^{\boldsymbol{\top}} \mathbf{J}_{\boldsymbol{\gamma}}\) 可以这样分解的度量,是马氏度量(Mahalanobis distance)的定义,也进一步导出了黎曼度量,即对于任意隐空间中的 \(\mathcal{Z}\),黎曼度量 \(\mathcal{M}: \mathcal{Z} \rightarrow \mathcal{R}^{d \times d}\) 把隐空间的任意点映射到一个正定对称矩阵上,那么由之前的变化可以看出,只要生成映射 \(f\) 足够光滑(在实践中这样的条件并不是很苛刻),由生成映射生成的流形就是黎曼流形,或者说一个具有光滑的内积结构的流形
那么有了这样一个流形之后,问题就变成了找到流形上两点的最短距离,或者说测地距离:
\[\gamma_{t}^{(\text {shortest) }}=\underset{\gamma_{t}}{\operatorname{argmin}} \text { Length }\left[f\left(\gamma_{t}\right)\right], \quad \gamma_{0}=\mathbf{z}_{0}, \quad \gamma_{1}=\mathbf{z}_{1} .\]下面的解由 Do Carmo (1992) 给出:
\[\begin{aligned} \gamma_{t}^{(\text {shortest) }} & = \underset{\boldsymbol{\gamma}_{t}}{\operatorname{argmin}} \int_{0}^{1} \sqrt{\left\langle\dot{\boldsymbol{\gamma}}_{t}, \mathbf{M}_{\boldsymbol{\gamma}_{t}} \dot{\boldsymbol{\gamma}}_{t}\right\rangle} \mathrm{d} t, \quad \boldsymbol{\gamma}(0)=\mathbf{x}, \boldsymbol{\gamma}(1)=\mathbf{y} \\ & \Leftrightarrow \underset{\boldsymbol{\gamma}_{t}}{\operatorname{argmin}} \int_{0}^{1}\left\langle\dot{\boldsymbol{\gamma}}_{t}, \mathbf{M}_{\boldsymbol{\gamma}_{t}} \dot{\boldsymbol{\gamma}}_{t}\right\rangle \mathrm{d} t, \quad \boldsymbol{\gamma}(0)=\mathbf{x}, \boldsymbol{\gamma}(1)=\mathbf{y} \\ & \; \Big\Updownarrow \quad L\left(\gamma_{t}, \dot{\gamma}_{t}, \mathbf{M}_{\gamma_{t}}\right) = \left\langle\dot{\gamma}_{t}, \mathbf{M}_{\gamma_{t}} \dot{\gamma}_{t}\right\rangle=\sum_{i=1}^{d} \sum_{j=1}^{d} \dot{\gamma}_{t}^{(i)} \cdot \dot{\gamma}_{t}^{(j)} \cdot M_{\gamma_{t}}^{(i j)}=\left(\dot{\gamma}_{t} \otimes \dot{\gamma}_{t}\right)^{\top} \operatorname{vec}\left[\mathbf{M}_{\gamma_{t}}\right] \\ &= \underset{\boldsymbol{\gamma}_{t}}{\operatorname{argmin}} \int_{0}^{1} \left(\dot{\gamma}_{t} \otimes \dot{\gamma}_{t}\right)^{\top} \operatorname{vec}\left[\mathbf{M}_{\gamma_{t}}\right]\mathrm{d} t, \quad \boldsymbol{\gamma}(0)=\mathbf{x}, \boldsymbol{\gamma}(1)=\mathbf{y} \end{aligned}\]通过 Euler-Lagrange Equation 可知:
\[\begin{aligned} \frac{\partial L}{\partial \gamma_{t}} & =\frac{\partial}{\partial t} \frac{\partial L}{\partial \dot{\gamma}_{t}} \\ & =\frac{\partial}{\partial t} \frac{\partial\left\langle\dot{\gamma}_{t}, \mathbf{M}_{\gamma_{t}} \dot{\gamma}_{t}\right\rangle}{\partial \dot{\gamma}_{t}}=\frac{\partial}{\partial t}\left(2 \cdot \mathbf{M}_{\gamma_{t}} \dot{\gamma}_{t}\right)=2\left[\frac{\partial \mathbf{M}_{\gamma_{t}}}{\partial t} \dot{\gamma}_{t}+\mathbf{M}_{\gamma_{t}} \ddot{\gamma}_{t}\right] \\ & \; \Bigg\Updownarrow \; \frac{\partial \mathbf{M}_{\boldsymbol{\gamma}_{t}}}{\partial t}=\left[\begin{array}{cccc} \frac{\partial M_{\gamma t}^{(11)}}{\partial t} & \cdots & \frac{\partial M_{\gamma t}^{(1 D)}}{\partial t} \\ \frac{\partial M_{\gamma t}^{(21)}}{\partial t} & \cdots & \frac{\partial M_{\gamma t}^{(2 D)}}{\partial t} \\ \vdots & \ddots & \vdots \\ \frac{\partial M_{\gamma}^{(D 1)}}{\partial t} & \cdots & \frac{\partial M_{\gamma t}^{(D D)}}{\partial t} \end{array}\right]=\left[\begin{array}{cccc} \frac{\partial M_{\gamma t}^{(11)\mathbf{T}} }{\partial \gamma_{t}} \dot{\gamma}_{t} & \cdots & \frac{\partial M_{\gamma t}^{(1 D) \mathbf{T}} }{\partial \gamma_{t}} \dot{\gamma}_{t} \\ \frac{\partial M_{\gamma t}^{(21)\mathbf{T}} }{\partial \gamma_{t}} \dot{\gamma}_{t} & \cdots & \frac{\partial M_{\gamma}^{(2 D)\mathbf{T}} }{\partial \gamma_{t}} \dot{\gamma}_{t} \\ \vdots & \ddots & \vdots \\ \frac{\partial M_{\gamma t}^{(D 1)\mathbf{T}}}{\partial \gamma_{t}} \dot{\gamma}_{t} & \cdots & \frac{\partial M_{\gamma t}^{(D D)\mathbf{T}}}{\partial \gamma_{t}} \dot{\gamma}_{t} \end{array}\right] \\ & =2\left[\left(\mathbb{I}_{d} \otimes \dot{\gamma}_{t}^{\top}\right) \frac{\partial \mathrm{vec}\left[\mathbf{M}_{\gamma_{t}}\right]}{\partial \gamma_{t}} \dot{\gamma}_{t}+\mathbf{M}_{\gamma_{t}} \ddot{\gamma}_{t}\right] \\ \end{aligned}\]因此得出最短距离符合一个微分方程,可以通过数值计算求解:
\[\ddot{\gamma}_{t}=-\frac{1}{2} \mathbf{M}_{\gamma_{t}}^{-1}\left[2\left(\mathbb{I}_{d} \otimes \dot{\gamma}_{t}^{\top}\right) \frac{\partial \operatorname{vec}\left[\mathbf{M}_{\gamma_{t}}\right]}{\partial \gamma_{t}} \dot{\gamma}_{t}-\frac{\partial \operatorname{vec}\left[\mathbf{M}_{\gamma_{t}}\right]^{\top}}{\partial \gamma_{t}}\left(\dot{\gamma}_{t} \otimes \dot{\gamma}_{t}\right)\right]\]如下图估算出 \(\mathbf{x} = f(\mathbf{z})\) 可以计算出测地距离:
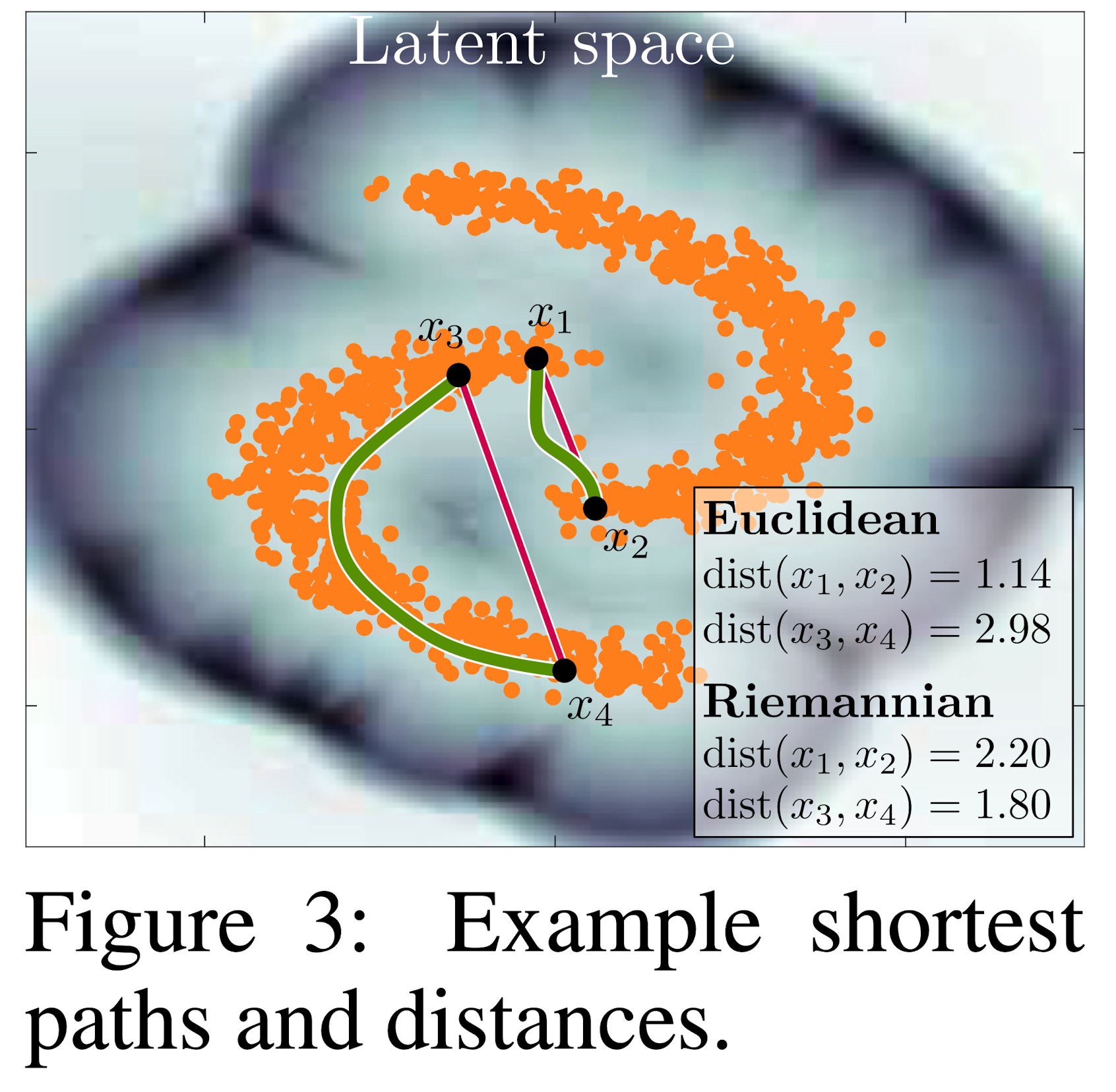
1.2. Stochastic Generative Model
与之前的确定的映射相对应的,就是有随机噪声的映射,这也是一众SOTA的生成模型的基础,可以这样理解:在现实世界中的一切数据都是有噪声的,比起完美的每个点都在由确定性映射 \(\mathbf{x}=f(\mathbf{z})\) 定义的流形上,真实数据的情况更应当是在流形附近,因此如下定义一个带有噪声的生成模型(Stochastic Generative Model)
\[f(\mathbf{z})=\boldsymbol{\mu}(\mathbf{z})+\boldsymbol{\sigma}(\mathbf{z}) \odot \boldsymbol{\epsilon}, \quad \boldsymbol{\mu}: \mathcal{Z} \rightarrow \mathcal{X}, \boldsymbol{\sigma}: \mathcal{Z} \rightarrow \mathbb{R}_{+}^{D}, \boldsymbol{\epsilon} \sim \mathcal{N}\left(\mathbf{0}, \mathbb{I}_{D}\right)\]类似 VAE 的 Reparameterization Trick 中的无偏统计量,可以定义随机生成模型的度量 \(\overline{\mathbf{M}}_{\mathbf{z}}\) 为其证明在本文不表
\[\overline{\mathbf{M}}_{\mathbf{z}}=\mathbb{E}_{p(\epsilon)}\left[\mathbf{M}_{\mathbf{z}}\right]=\left(\mathbf{J}_{\mathbf{z}}^{(\mu)}\right)^{\top}\left(\mathbf{J}_{\mathbf{z}}^{(\boldsymbol{\mu})}\right)+\left(\mathbf{J}_{\mathbf{z}}^{(\boldsymbol{\sigma})}\right)^{\top}\left(\mathbf{J}_{\mathbf{z}}^{(\boldsymbol{\sigma})}\right)\]下面以 VAE 为例子说明随机生成模型的作用方法:VAE 有一个先验分布 \(p(\mathbf{z})=\mathcal{N}\left(\mathbf{0}, \mathbb{I}_{d}\right)\),作为隐空间采样的分布,然后采样的点 \(\mathbf{z}\) 通过映射 \(\boldsymbol{\mu}_{\theta}: \mathcal{Z} \rightarrow \mathcal{X},\boldsymbol{\sigma}_{\theta}:\mathcal{Z} \rightarrow \mathbb{R}_{+}^{D}\) 映回到数据空间 \(\mathcal{X}\) ,在此之上再加了一个噪声:
\[\mathbf{x}=\boldsymbol{\mu}_{\theta}(\mathbf{z})+\boldsymbol{\sigma}_{\theta} \odot \boldsymbol{\epsilon},\epsilon \sim \mathcal{N}\left(\mathbf{0}, \mathbb{I}_{D}\right)\]为了训练 VAE,需要知道编码器的真实分布 \(p_{\theta}(\mathbf{z} \mid \mathbf{x})\),但是由于真实分布不可处理性,用一个 \(q_{\phi}(\mathbf{z} \mid \mathbf{x})=\mathcal{N}\left(\mathbf{z} \mid \boldsymbol{\mu}_{\phi}(\mathbf{x}), \mathbb{I}_{d} \boldsymbol{\sigma}_{\phi}^{2}(\mathbf{x})\right)\) 逼近,其参数用神经网络给出,优化目标是 ELBO,是 \(\log(p(\mathbf{x}))\) 的下逼近(由Jenson不等式得到,详细推导见 VAE笔记
\[\left\{\theta^{*}, \phi^{*}\right\}=\underset{\theta, \phi}{\operatorname{argmax}} \mathbb{E}_{q_{\phi}(\mathbf{z} \mid \mathbf{x})}\left[\log \left(p_{\theta}(\mathbf{x} \mid \mathbf{z})\right)\right]-\mathrm{KL}\left(q_{\phi}(\mathbf{z} \mid \mathbf{x}) \| p(\mathbf{z})\right)\]2. From an Optimal Transport Point of View
由最优传输理论定义的 \(Wassterstein\) 距离,有两个非常好的性质:
- \(Wassterstein\) 距离是一个“弱距离”,可以比较一个离散分布和一个连续分布之间的距离,经验分布模型往往用 \(\nu \stackrel{\text { def. }}{=} \frac{1}{n} \sum_{j=1}^{n} \delta_{y_{j}} ,y_{j} \in \mathcal{X} \subset \mathbb{R}^{p}\) 表示,而生成模型通过参数 \(\theta\) 定义一个连续分布 \(\left(\mu_{\theta}\right)_{\theta \in \Theta} \subset \mathcal{P}(\mathcal{X}), \Theta \subset \mathbb{R} q\)
- 比起传统的 \(KL\) 散度,\(Wassterstein\) 距离还能够比较两个支撑集无交的分布之间的距离
总之就是 \(Wasserstein\) 距离有很多好处,为了使用之,在最优传输理论框架下,研究生成模型是有意义的:
有分布 \(\mu, \nu\),同时有传输代价;\(c(x,y):\mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R}\),可以定义\(Wassterstein\) 距离 \(W_{c}(\mu, \nu)\):
\[W_{c}(\mu, \nu)=\min _{\gamma \in \mathcal{P}(\mathcal{X} \times \mathcal{X})}\left\{\int_{\mathcal{X} \times \mathcal{X}} c(x, y) \mathrm{d} \gamma(x, y) ; P_{1 \#} \gamma=\mu, P_{2 \#}\gamma=\nu\right\}\]其中 \(P_{1 \#}\) 为通过投影函数 \( P_{1}(x, y)=x\) 诱导的前向算子(把分布整体 \(\gamma\) ,在投影前后质量不变的条件下的算子),而这样投影函数诱导的前向算子其实是映射到 \(\gamma\) 的边际分布上,详细定义见 OT-Notes1 中的定义,这里稍微带一笔:
对于生成映射 \(g: \mathcal{Z} \rightarrow \mathcal{X}\),设想一个把分布中的所有点一起映射的映射 \(g_{\#}\),同时通过测度 \(\zeta \in \mathcal{P}(\mathcal{Z})\) ,要求其映射前后的质量不变,\(\forall B \subset \mathcal{X},\left(g_{\text {# }} \zeta\right)(B) \stackrel{\text { def. }}{=} \zeta\left(g^{-1}(B)\right)=\zeta(\{z \in \mathcal{Z} ; g(z) \in B\})\)
下图中左图形象的展示了低维流形嵌入到高维数据空间,数据集生成离散的经验分布函数,而生成模型的任务就是通过控制参数 \(\theta\) 最优化经验分布 \(\nu =\frac{1}{n} \sum_{j=1}^{n} \delta_{x_{j}}\) 和 \(g_{\#} \zeta\) 的 \(Wasserstein\) 距离 \(W_{c}(g_{\theta \# } \zeta, \nu)\),即
\[\begin{aligned} \theta^{*} &= \arg \min _{\theta} E(\theta) = W_{c}\left(g_{\theta \# } \zeta, \nu\right) \\ &= \min _{\gamma \in \mathcal{P}(\mathcal{X} \times \mathcal{X})}\left\{\int_{\mathcal{X} \times \mathcal{X}} c(x, y) \mathrm{d} \gamma(x, y) ; P_{1 \#} \gamma =\zeta, P_{2 \#}\gamma=\nu\right\} \end{aligned}\]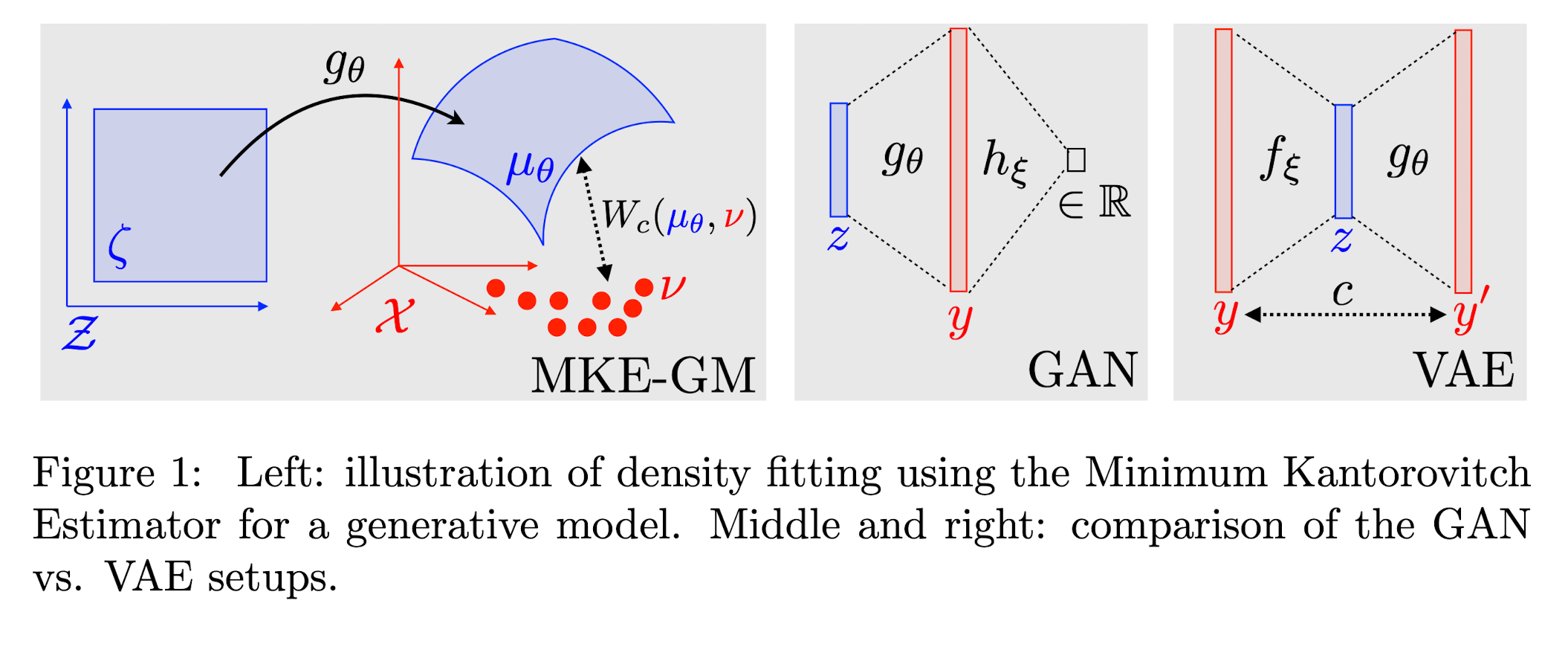
那么现在讨论在最优传输的框架下,讨论两个 SOTA 的生成模型,GAN 和 VAE。这两个模型最大的区别在于,VAE保留了隐空间 \(\mathbf{Z}\) 和数据空间 \(\mathcal{X}\) 之间的联系,换言之,隐空间的低维流形嵌入到数据空间空间的过程同样可以用一个前向算子 \(g_{\#}\) 表达;与之相对应的,GAN 放弃了对于用前向算子 \(g_{\#}\) 建立隐空间与数据空间之间的联系,转向去寻求利用生成器和判别器在高维空间中的对抗来训练一个好的生成器 \(g\)
2.2. Dual Formulation and GAN
这里姑且当作在读的人对于 GAN 有一定的了解,GAN 训练生成器 \(g:\mathbf{Z} \rightarrow \mathcal{X}\) ,把隐空间中采样映射到数据空间 \(\mathcal{X}\) 中,去和经验函数 \(\nu =\frac{1}{n} \sum_{j=1}^{n} \delta_{x_{j}}\) 近似的数据分布 \(P(X)\) ,那么 GAN 模型,在最优传输框架下描述就是去解:
\[g_\theta^* = \arg \min _{\theta} W_{c}\left(g_{\theta\# } \zeta, \nu\right)\]这是一个 \(Kantorvich\) 形式的最优传输问题,由 \(Kantorvich\) 对偶性得出:
\[\begin{aligned} W_{c}\left(g_{\theta \# } \zeta, \nu\right) &= \min _{\gamma \in \mathcal{P}(\mathcal{X} \times \mathcal{X})}\left\{\int_{\mathcal{X} \times \mathcal{X}} c(x, y) \mathrm{d} \gamma(x, y) ; P_{1 \#} \gamma=\zeta , P_{2 \#}\gamma=\nu\right\}\ \\ &= \max _{h, \tilde{h}}\left\{\int_{\mathcal{Z}} h\left(g_{\theta}(z)\right) \mathrm{d} \zeta(z)+\int_{\mathcal{X}} \tilde{h}(y) \mathrm{d} \nu(y) ; \; h(x)+\tilde{h}(y) \leqslant c(x, y)\right\} \end{aligned}\]这样就可以显式的通过梯度下降优化 \(\theta\):
\[\nabla E(\theta)=\int_{\mathcal{Z}}\left[\partial_{\theta} g_{\theta}(z)\right]^{\top} \nabla h^{\star}\left(g_{\theta}(z)\right) \mathrm{d} \zeta(z)\]\(h^{\star}\) 是一个\(Kantorvich\) 对偶的最优解,且值得一提的是,由于 \((h, \tilde{h})\) 总是可以通过把 \(\tilde{h}\) 换成 \(h^c\) 的 \(c-tranform\) 提升
\[h^{c}(y) \stackrel{\text { def. }}{=} \max _{x} c(x, y)-h(x)\]也就是说解 \((h, \tilde{h})\) 和解一个 \(h\) 是一样的
进一步,为了解出 GAN 形式下的 \(Kantorvich\) 对偶问题,有两种方案:
-
放弃给出一个连续的 \(h\),换一个离散的 \(\tilde{h} = \left(\tilde{h}\left(y_{j}\right)\right)_{j} \in \mathbb{R}^{n}\) ,同时利用 \(c-tranform\) 变换 \(h=(\tilde{h})^{c}\) ,这样就可以进行梯度下降计算
-
使用神经网络拟合一个连续的 \(h=h_{\xi}: \mathcal{X} \rightarrow \mathbb{R}\),\(h_{\xi}\) 其实是充当 GAN 中的判别器,代入 \(W_{c}\left(g_{\theta \# } \zeta, \nu\right)\) 的定义中有
\[\min _{\theta} \max _{\xi} \int_{\mathcal{Z}} h_{\xi} \circ g_{\xi}(z) \mathrm{d} \zeta(z)+\sum_{j} h_{\xi}^{c}\left(y_{j}\right)\]通过这个 \(Min-Max\) 问题也正是 WGAN 的定义,而其中通过一些输出的限制使得 \(h=h_{\xi} \in [0,1]\)
2.2. Primal Formulation and VAE
生成模型 \(\mu_{\theta}=g_{\theta_{H}} \zeta\),当限制在 \(\pi \in \mathcal{P}(\mathcal{Z} \times \mathcal{X})\) ,就是 VAE 的形式了(指VAE的思想)
\[E(\theta)=\min _{\pi \in \mathcal{P}(\mathcal{Z} \times \mathcal{X})}\left\{\int_{\mathcal{Z} \times \mathcal{X}} c\left(g_{\theta}(z), y\right) \mathrm{d} \pi(z, y) ; P_{1 \#} \pi=\zeta, P_{2 \#} \pi=\nu\right\}\]同样的,在 VAE 的最优传输提法中,在优化的约束中,不出现 \(\theta\),可以直接优化 \(E(\theta)\):
\[\nabla E(\theta)=\int_{\mathcal{Z} \times \mathcal{X}}\left[\partial_{\theta} g_{\theta}(z)\right]^{\top} \nabla_{1} c\left(g_{\theta}(z), y\right) \mathrm{d} \pi^{\star}(z, y)\]其中 \(\pi^{\star}\) 是 VAE 隐空间的低维流形和数据空间的经验分布的最优传输的解,为了具体的解上面的优化问题,比较简单的构造 \(coupling \; \pi\) 的方法就是限制到一个离散分布上:
\[\pi_{\xi} \stackrel{\text { def. }}{=} \sum_{j} \delta_{\left(f_{\xi}\left(y_{j}\right), y_{j}\right)} \in \mathcal{P}(\mathcal{Z} \times \mathcal{X})\]其中 \(f_{\xi}: \mathcal{X} \rightarrow \mathcal{Z}\) 可以视作一个编码器,但是这样一个离散的编码器往往做不到限制中要求的 \(P_{1 \#} \pi=\zeta\),那么弱化这一条变成最小化投影分布和 \(\zeta\) 之间的距离,即 \(\min D\left(P_{1 \#} \pi \mid \zeta\right)\) ,加入到代价函数中得:
\[E_{\lambda}(\theta)=\min _{\pi}\left\{\int_{\mathcal{Z} \times \mathcal{X}} c\left(g_{\theta}(z), y\right) \mathrm{d} \pi(z, y)+\lambda D\left(P_{1 \#} \pi \mid \zeta\right) ; P_{2 \#} \pi=\nu\right\}\]这和 VAE 中要求的最大化 ELBO:\(\mathcal{L}_{\boldsymbol{\theta}, \boldsymbol{\phi}}(\mathbf{x}) = \mathbb{E}_{q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})}\left[\log p_{\boldsymbol{\theta}}(\mathbf{x}\mid \mathbf{z})+\log [p_{\boldsymbol{\theta}}(\mathbf{z}) / q_{\boldsymbol{\phi}}(\mathbf{z} \mid \mathbf{x})] \right]\) 是几乎等价的,第一部分要求的是最小化化编码器分布和经验分布的距离,第二项要求在隐空间中,先验分布 \(\zeta\) 和编码器分布 \(q\) 不是很远
Reference
- Aude Genevay , Gabriel Peyre , Marco Cuturi (2017) “GAN and VAE from an Optimal Transport Point of View”
- Georgios Arvanitidis, Lars Kai Hansen, Søren Hauberg (2017) “LATENT SPACE ODDITY: ON THE CURVATURE OF DEEP GENERATIVE MODELS”
- Matthew Thorpe (2018) “Introduction to Optimal Transportation”
- Diederik P. Kingma and Max Welling (2019), “An Introduction to Variational Autoencoders”, Foundations and TrendsR in Machine Learning”